Trigonometry for SSC CGL: Formula, Tricks, Questions

SSC CGL Trigonometry

Trigonometry is one of the most significant branches of mathematics, with numerous applications in a wide range of fields. The study of the relationship between the sides and angles of a right-angle triangle is the focus of the Trigonometry branch. As a result, using trigonometric formulas, functions, or trigonometric identities, it is possible to find the missing or unknown angles or sides of a right triangle. Angles in trigonometry can be measured in degrees or radians. 0°, 30°, 45°, 60°, and 90° are some of the most widely utilized trigonometric angles for calculations.

In this blog, we are going to provide complete Trigonometry notes for SSC CGL including formulas and questions. Let’s begin!

Trigonometry Formulas for SSC CGL

There are 6 main Trigonometric functions namely, Sin, Cos, Tan, Sec, Cosec, and Cot. All Trigonometric functions, formulas and tricks are derived from these 6 functions. Below is the list of important Trigonometry formulas for SSC CGL 2023 and other competitive exams.

Let’s start with the values of different angles in different quadrants:

(1) In the hexadecimal system, the angles are measured in degrees, minutes and seconds.

One complete rotation = 360 degrees (360⁰) 1⁰ = 60 minutes (60’); 1’ = 60 seconds (60”)

In the circular system, the angles are measured in radians. π radians (π^c) = 180⁰

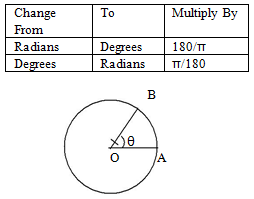
(2) Let S = length of arc AB

θ = angle AOB expressed in radians and r = radius of the circle

Then, S = r × θ

(3) And the area of sector AOB is A = (1/2) × r² × θ

(4) Consider the right angle triangle ABC as shown

Sine θ = Opposite Side/Hypotenuse = BC/AC

Cosine θ = Adjacent Side/Hypotenuse = AB/AC

Tangent θ = Opposite Side/Adjacent Side = BC /AB

Cosec θ = 1/sinθ

Sec θ = 1/cos θ

Cot θ = 1/tan θ

(5) Limiting Value of the Trigonometrical Ratios 

1. Since sin² θ + cos² θ = 1, hence each of sin θ and cos θ is numerically less than 1; or their maximum value is 1.
2. Since sec θ and cosec θ are respectively reciprocals of cos θ and sin θ, therefore the values of sec θ and cosec θ are always greater than 1; or their minimum value is 1.
3. tan θ and cot θ can have any value between – infinity and + infinity.

(6) Signs Of Trigonometrical Ratios

1. Quadrant: 0 to 90, All + ve

2. Quadrant: 90° to 180°, only sin θ and cosec θ + ve, rest – ve

3. Quadrant: 180° to 270°, only tan θ and cot θ + ve, rest – ve

4. Quadrant: 270° to 360°, only cos θ and sec θ + ve, rest – ve

(7) Trigonometrical Ratios Of Allied Angles 

1. sin ( – θ) = – sin θ; cosec (- θ) = – cosec θ

cos ( – θ) = cos θ; sec (- θ) = sec θ;

tan ( – θ) = – tan θ; cot (- θ) = – cot θ

2. Trigonometric ratios of (90° – θ) in terms of those of θ, for all values of θ:

sin (90° – θ) = cos θ; cosec (90° – θ) = sec θ

cos (90° – θ) = sin θ; cosec (90° – θ) = cosec θ

tan(90° – θ) = cot θ; cot (90° – θ) = tan θ

 3. sin (90° + θ) = cos θ; cosec (90° + θ) = sec θ

cos (90° + θ) = – sin θ; cosec (90° + θ) = – cosec θ

tan(90° + θ) = – cot θ; cot (90° + θ) = tan θ

 4. sin (180° – θ) = cos θ; cosec (180° – θ) = cosec θ

cos (180° – θ) = – cos θ; cosec (180° – θ) = sec θ

tan(180° – θ) = – tan θ; cot (90° -θ) = – cot θ

Important Points:

1. Since angles 360° – θ and (- θ) are coterminal angles, the trigonometric ratios of (360° – θ) and (- θ) must be identical.
2. Since angles 360° – θ and θ are coterminal angles, the trigonometric ratios of 360° + θ and θ must be identical.

Maximum and Minimum Value Trigonometric Identity:

Type-I: 

In case of sec²x, cosec²x, cot²x and tan²x, we cannot find the maximum value because they can have infinity as their maximum value. So in question containing these trigonometric identities, you will be asked to find the minimum values only. The typical question forms are listed below:

Example: -1

Find the Minimum value of 9 cos ²x + 2 sec ²x

sol – this equation is a typical example of our type-3 so apply the formula 2√ ab so,

• Minimum Value = 2√ 9 x 2= 2√ 18

Example:-2

Find the Minimum value of 8 tan ²x + 7 cot ²x
sol – this equation is a typical example of our type-3 so apply the formula 2√ ab so,

• Minimum Value = 2√ 8 x 7= 2√ 56

Type -II:

Example -1

Find the Maximum and Minimum Value of 3 sin x + 4 cos y

Sol- If you find the question of this kind, apply the above formulae.

• Maximum Value = √ 9 + 16 = √ 25 = 5
• Minimum Value = – √ 9 + 16 = – √ 25 = – 5

Example-2

Find the Maximum and Minimum Value of 3 sin x + 2 cos y

Sol- If you find the question of this kind, apply the above formulae.

• Maximum Value = √ 9 + 4 = √ 13
• Minimum Value = – √ 9 + 4 = – √ 13

Type III:

Example -1

Find the maximum and Minimum Value of 3 sin ²x + 4 cos ²x

Sol- Here the 4> 3 so

•  Maximum Value = 4
• Minimum Value = 3 

Example –2

Find the maximum and Minimum Value of 5 sin ²x + 3 cos ²x

Sol – Here 5>3

• Maximum Value = 5
• Minimum Value = 3

Type-IV

Find the Minimum Value of Sec ²x + cosec ²x

Sol – 1 + tan ²x + cosec ²x  ——————————————–(Sec ²x = 1 + tan ²x)

= 1+ tan ²x + 1 + cot ²x ————————————————(cosec ²x = 1 + cot ²x )

=2 + tan ²x + cot ²x—————————————————apply type-3 formula

=2 + 2 √ 1 x 1 = 2 + 2 =4

SSC CGL Trigonometry Questions

Below we are going to provide you all with the important SSC CGL Trigonometry questions. These are the types of questions that are asked in the CGL and other Government examinations.

1. Evaluate : ( Cot⁴ Θ – Cosec⁴ Θ + Cot² Θ + Cosec² Θ ) 

A. 1
B. 0
C. -1
D. 2

Correct Answer: B

 2. If 7 sin² Θ + 3 cos² Θ = 4 and 0 ≤ Θ ≤ π/2, then the value of tan Θ is :

A. √3/7
B. √2/7
C. 1/√3
D. 1/√7

Correct Answer: C

3. If x = a cos³ Θ, y = b sin³ Θ, then
(x/a)^2/3 +(y/b)^2/3 = ?

A. 1
B. 0
C. 2
D. 4

Correct Answer: A

4. The value of cot 2π/20 x cot 4π/20 x cot 5π/20 x cot 6π/20 x cot 8π/20 is