Important Notes & Short Tricks on Trigonometric Identities

Important Short Tricks on Trigonometric Identities

Pythagorean Identities

• sin² θ + cos² θ = 1
• tan² θ + 1 = sec² θ
• cot² θ + 1 = cosec² θ

Negative of a Function

• sin (–x) = –sin x
• cos (–x) = cos x
• tan (–x) = –tan x
• cosec (–x) = –cosec x
• sec (–x) = sec x
• cot (–x) = –cot x

If A + B = 90^o, Then

• Sin A = Cos B
• Sin²A + Sin²B = Cos²A + Cos²B = 1
• Tan A = Cot B
• Sec A = Cosec B

For example:    

If tan (x+y) tan (x-y) = 1, then find tan (2x/3)?

Solution: 

If A+B = 90°, then       

Tan A = Cot B or Tan A×Tan B = 1

So, A +B = 90^o

(x+y)+(x-y) = 90^o, 2x = 90^o , x = 45^o

Tan (2x/3) = tan 30^o = 1/√3

If A – B = 90^o, and (A › B) Then,

• Sin A = Cos B
• Cos A = – Sin B
• Tan A = – Cot B
• Cosec A = – Sec B
• Sec A = Cosec B

If A ± B = 180^o, then

• Cos A = – Cos B

If A + B = 180^o                   

Then,

• Sin A = Sin B
• tan A = – tan B

If A – B = 180^o                    

Then,

• Sin A = – Sin B
• tan A = tan B

 If A + B + C = 180^o, then

Tan A + Tan B +Tan C = Tan A * Tan B *Tan C

 

sin θ * sin 2θ * sin 4θ = ¼ sin 3θ

cos θ * cos 2θ * cos 4θ = ¼ cos 3θ

For Example: What is the value of cos 20^o cos 40^o cos 60^o cos 80^o?

Solution: We know, cos θ * cos 2θ * cos 4θ = ¼ cos 3θ

Now, (cos 20^o cos 40^o cos 80^o ) cos 60^o

¼ (Cos 3*20) * cos 60^o

¼ Cos² 60^o = ¼ * (½)² = 1/16

If  a sin θ + b cos θ = m     &    a cos θ – b sin θ = n

then a² + b² = m² + n²

For Example:

If 4 sin θ + 3 cos θ = 2 , then find the value of  4 cos θ – 3 sin θ:

Solution:

Let 4 cos θ – 3 sin θ = x

By using formulae a² + b² = m² + n²

4² + 3² = 2² + x²

16 + 9 = 4 + x²

X = √21

If

sin θ +  cos θ = p     &     cosec θ + sec θ = q

then p – (1/p) = 2/q

For Example:

If sin θ + cos θ = √2 , then find the value of  cosec θ + sec θ:

Solution:

By using formulae:

P – (1/p) = 2/q

√2-(1/√2) = 1/√2 = 2/q

q = 2√2 or cosec θ + sec θ = 2√2

If

a cot θ + b cosec θ = m     &    a cosec θ + b cot θ = n

then b² – a²  = m² – n²

If

cot θ + cos θ = x     &    cot θ – cos θ = y

then x² – y² = 4 √xy

If

tan θ + sin θ = x     &    tan θ – sin θ = y

then x² – y² = 4 √xy

If

y = a² sin²x + b² cosec²x + c

y = a² cos²x + b² sec²x + c

y = a² tan²x + b² cot²x + c

then,

y_min = 2ab + c

y_max = not defined

For Example:                    

If y = 9 sin² x + 16 cosec² x + 4 then y_min is:

Solution:            

For, y min = 2* √9 * √16 + 4

= 2*3*4 + 20 = 24 + 4 = 28

If            

y = a sin x + b cos x + c

y = a tan x + b cot x + c

y = a sec x + b cosec x + c

then,     y_min = – [√(a²+b²)] + c

y_max = + [√(a²+b²)] + c

For Example:                    

If y = 1/(12sin x + 5 cos x +20) then y_max is:

Solution:            

For, y max = 1/x min

= 1/[- (√12² +5²) +20] = 1/(-13+20) = 1/7

Sin² θ, maxima value = 1, minima value = 0

Cos² θ, maxima value = 1, minima value = 0

Here are some important questions of Trigonometric identities.

(1)Value of  is

(a)

(b)

(c)

(d)None of these

Ans.(a)

 is equal to

 

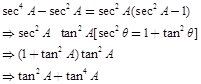
(2)If is acute and  then  is equal to

(a)

(b)3

(c)  2

(d)  4

Ans.  (c)

If sum of the inversely proportional value is 2

i.e if .  then

 

so =2

or we can put = 45°

(3)The simplified value of(Secx Secy + tanx tany)² – (Secx tany + tanx Secy)² is

(a)-1

(b)0

(c)sec²x

(d)1

Ans. (d)

The simplified value of (Secx Secy + tanx tany)² – (Secx tany + tanx Secy)² is obtained by putting x = y = 45°

= (√2×√2 + 1×1)² – (√2×1 + 1×√2)²

= (2+1)² – (√2+√2)²

=(3)² – (2√2)²

= 9 – 8 = 1

(4) Find the value of 

(a)  1

(b)  -1

(c)  2

(d)  -2

Ans. (c)

put 

(5) If  then  is equal

(a)7/4

(b) 7/2

(c)5/2

(d)5/4

Ans. (d)

 as we know that

on solving we get sec= 5/4

Note: if x+y=a

and x-y=b

then x=(a+b)/2 and y=(x-y)/2

More from us:

More from us:

SSC CGL Previous Question Papers PDF in Hindi & English

SSC CGL Syllabus & Exam Pattern