- Home/
- SSC & Railways/
- SSC CGL/
- Article
Important Notes & Short Tricks on Height & Distance with Questions for SSC Exams 2023
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Heights and Distance is a study of Trigonometry applications. It has various real-world uses, such as measuring the height of an object, the depth of an object, the distance between two celestial objects, and so on. Trigonometric formulas and ratios are useful in the study of heights and distances.
In this post, we will talk about heights and distances basics, short tricks along with some important questions.
Table of content
Trigonometry is one of the important chapters for the upcoming SSC & Railways exams 2023. We will be covering a very important topic Height & Distance from this section. It is important to learn the basics of this topic before moving further.
Some of the important terms associated with Height & Distance are as follows:
- Line of Sight
- Angle of Elevation
- Angle of Depression
Line of Sight
The line of sight is the imaginary line drawn from the observer’s eye to an item. It indicates where an observer’s gaze is directed. Furthermore, the line of sight indicates the type of inclination angle established with horizontal.
Angle of Elevation
The angle of elevation is the angle produced by the line of sight with the horizontal when the observer is looking up at an object. When the viewer raises his head over the horizontal line, this angle is generated.
Angle of Depression
It is the angle of inclination formed by the line of sight with the horizontal when the observer is viewing the object downwards. This angle is formed when the observer lowers his head downwards from the top to the ground.
Trigonometric Ratio
Trigonometric ratios are used to address height and distance problems. We know that the angle’s trigonometric ratio gives the relationship between any two sides of a triangle. Let us go over all of the trigonometric ratios in depth.

Some specific Ratios are as follows:
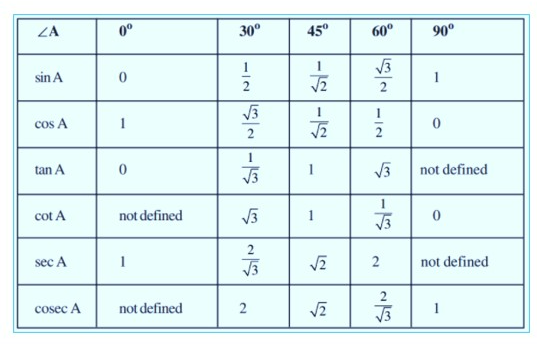
Short Tricks on Height & Distance with Questions
Angle of Elevation: Let AB be a tower/pillar/shell/minar/pole etc.) standing at any point C on the level ground is viewing at A.
The angle, which the line AC makes with the horizontal line BC is called the angle of elevation .so angle ACB is the angle of elevation.
Angle of Depression: If an observer is at Q and is viewing an object R on the ground, then the angle between PQ and QR is the angle of depression .so angle PQR is the angle of depression.
Numerically angle of elevation is equal to the angle of depression.
Both angles are measured with the horizontal.
- The thread of a kite is 120 m long and it is making 30° angular elevation with the ground. What is the height of the kite?
Solution:
Sin 30° = h/120
1/2 = h/120
h = 60m
- A tree bent by the wind. The top of the tree meets the ground at an angle of 60°.If the distance between the top of the foot is 8 m then what was the height of the tree?
Solution:
tan 60° = x/8
√3 = x/8
x = 8 √3
y cos 60° = 8/y
1/2 = 8/y
y = 16
therefore the height of the tree = x+y
= 8√3+16
= 8(√3+2)
- The angle of elevation of the top of a tower from a point on the ground is 30°. On walking 100m towards the tower the angle of elevation changes to 60°. Find the height of the tower.
Solution:
In right triangle ABD,
tan 60° = h/x
√3 x = h
x = h/√3
Again , in right triangle ABC ,
tan 30 = h/x+100
1/√3 = h/x+100
√3 h = x+100
√3 h = h/√3 + 100
√3 h – h/√3 =100
3 h – h/√3 =100
2 h = 100√3
h = 50√3
By short trick:
d = h (cot Ɵ1 – cot Ɵ2)
h = 100/(√3-1/√3) = 100*√3/2 = 50√3
Ɵ1 = small angle
Ɵ2 = large angle
d = distance between two places
h = height
- From the top of a temple near a river the angles of depression of both the banks of river are 45° & 30°. If the height of the temple is 100 m then find out the width of the river.
Solution:
tan 45° = AB/BD
1 = 100/BD
BD = 100
tan 30 ° = AB/BC
1/√3 = 100/BC
BC = 100 √3
Width of the river , CD = BC – BD = 100 (√3-1)
When the height of the tower is 1 m then the width of the river is √3-1
Since the height of the tower is 100 m
Therefore,
Width of river is 100(√3-1)m
By short trick:
The same formula can be used in this question too i.e.
d= h (cot Ɵ1 – cot Ɵ2)
- The angle of elevation of the top of a tower from a point is 30 °. On walking 40 m towards the tower the angle changes to 45°.Find the height of the tower?
Solution:
tan 45° = AB/BD
1 = AB/1
Therefore AB = 1
tan 30° = AB/BC =>1/√3 = 1/BC
therefore BC= √3
Now CD =√3-1 m and the height of the tower is 1 m
1 m = 1/√3-1
Therefore 40 m = 1/√3-1.40 = 40/√3-1
= 20 (√3+1)m
By trick:
40 = h(√3-1)
H = 40/(√3-1) = 20 (√3+1)m
Important Height and Distance Questions for Upcoming SSC Exams 2023
Some important Height and Distance questions for upcoming SSC exams 2023 are as follows:
1. The angle of elevation of the top of a tower from the top of a building whose height is 680 m is 45° and the angle of elevation of the top of same tower from the foot of the same building is 60°. What is the height (in m) of the tower?
A. 340(3 + √3)
B. 310(3 – √3)
C. 310(3 + √3)
D. 340(3 – √3)
2. From the top of an upright pole 24![]() feet high, the angle of elevation of the top of an upright tower was 60°. If the foot of the pole was 60 feet away from the foot of the tower, what tall (in feet) was the tower?
feet high, the angle of elevation of the top of an upright tower was 60°. If the foot of the pole was 60 feet away from the foot of the tower, what tall (in feet) was the tower?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
3. From the top of an upright pole 17.75 m high, the angle of elevation of the top of an upright tower was 60°. If the tower was 57.75 m tall, how far away (in m) from the foot of the pole was the foot of the tower?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
4. Two ships are on the opposite of a light house such that all three of them are collinear. The angles of depression of the two ships from the top of the light house are 30° and 60°. If the ships are 230![]() m apart, then find the height of the light house (in m).
m apart, then find the height of the light house (in m).
A. 175.4
B. 165.2
C. 172.5
D. 180.5
5. An person 1.8 metre tall is ![]() metre away from a tower. If the angle of elevation from his eye to the top of the tower is 30 degree, then what is the height (in m) of the tower?
metre away from a tower. If the angle of elevation from his eye to the top of the tower is 30 degree, then what is the height (in m) of the tower?
A. 32.5
B. 37.8
C. 30.5
D. 31.8
6. A ladder of length 3.5 m just reaches the top of a wall. If the ladder makes an angle of 60° with the wall, then what is the height of the wall (in m)?
A. 1.75
B. 3.5![]()
C. ![]()
D. ![]()
7. The length of the shadow of a vertical tower on level ground increases by 8.4 m when the altitude of the sun changes from 45° to 30°. What is the height of the tower (in m)?
A. 4.2![]()
B. ![]()
C. ![]()
D. ![]()
8. Exactly midway between the foot of two towers P and Q, the angles of elevation of their tops are 45° and 60°, respectively. The ratio of the height of P and Q is:
A. ![]()
B. 3 : 1
C. 1 : 3
D. ![]()
9. From the top of a 195 m high cliff, the angles of depression of the top and bottom of a tower are 30° and 60°, respectively. Find the height of the tower (in m).
A. ![]()
B. 195
C. 130
D. 65
10. A kite is attached to a string. Find the length of the string (in m) when the height of the kite is 90m and the string makes an angle of 30° with the ground.
A. 180
B. ![]()
C. 45
D. ![]()
Hope this was useful to you.
Happy Learning
3 Crore+ Registered Aspirants | 2.5 Crore Downloads | 50,000+ Selections


