Thin Cylinders Study Notes for Mechanical Engineering

Thin Cylinders

Thin cylinders are defined as a cylinder with a diameter that is much greater than their wall thickness; in other words, a thin mechanical cylinder or vessel is defined as a cylinder with a wall thickness that is less than one-twentieth of its internal diameter. Consider a cylinder or vessel with d interior diameter and t thickness. This cylinder's wall thickness is either t > d/20, t/d 1/20, or d/t > 20. The above term classifies a vessel, shell, or cylinder as a thin cylinder. Radial stress is deemed negligible in a mechanical calculation utilizing a narrow cylinder. A thin pressure vessel is defined as a closed cylindrical or spherical container designed to hold or store fluids at a pressure substantially different from the ambient pressure. Thin cylinders are essentially used for creating MCQ-based questions in the GATE question paper. Pressure vessels can be classified as

(i) On the basis of the ratio of diameter to thickness

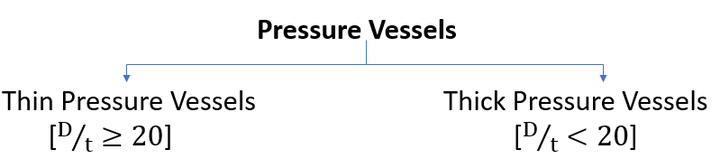
where D is the inner diameter of the shell & t is the thickness of the shell.

(ii) On the basis of the shape of the pressure vessel

However, Spherical pressure vessels are better, but cylindrical pressure vessels are most commonly used due to fabrication difficulty.

Common examples of pressure vessels are steam boilers, reservoirs, tanks, working chambers of engines, gas cylinders, etc.

Thin Cylindrical Shell Subject To Internal Pressure

Consider a thin cylinder of internal diameter d and wall thickness t, subject to internal gauge pressure P. The following stresses are induced in the cylinder
(a) Circumferential tensile stress (or hoop stress) σ_H.
(b) Longitudinal (or axial) tensile stress σ_L.
(c) Radial compressive stress σ_R, which varies from a value at the inner surface equal to the atmospheric pressure at the outside surface.

Assumptions in Thin-pressure Vessel

• Stresses are assumed to be distributed uniformly.
• The area is calculated considering the pressure vessel is thin
• Radial stresses are neglected
• A biaxial state of stress is assumed to be applicable

(a) Circumferential stress or Hoop stress, σ_H
There are normal stresses which act in the direction of circumference. These stresses are important as per the GATE exam. Due to internal fluid pressure, these are tensile in nature. In thin pressure vessels, hoop stresses are assumed to be uniform across the thickness.

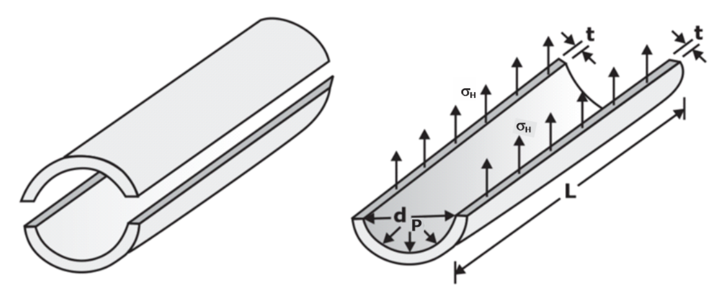
In the figure, we have shown one-half of the cylinder. This cylinder is subjected to an internal pressure P.

Pressure force by fluid ≤ Resisting force owing to hoop stresses σ_H
P x Projected Area ≤ 2.σ_h.L.t
P.d.L ≤ 2.σ_h.L.t

Pd/2t ≤ σ_h

for equilibrium, σ_h = Pd/2t

In η_L is the efficiency of the Longitudinal riveted joint,

σ_h = Pd/2tη_L

Similarly,

(b) Longitudinal stress (or axial stress) σ_L

Pressure force by fluid ≤ Resisting force owing to longitudinal stresses σ_L

P x (π/4)d² ≤ σ_L.π.d.t

Pd/4t ≤ σ_L

For equilibrium, σ_L= Pd/4t

In η_L is the efficiency of the circumferential riveted joint,

σ_L= Pd/4tη_C

Thus, the magnitude of the longitudinal stress is one-half of the circumferential stress, both the stresses being of tensile nature.

Hoop strain or Circumferential strain:

∈₁ = ∈_H = σ_L/E - µ(σ₂/E) = (1/E)(σ_H - µσ_L)

Δd/d = ∈_H = [Pd/4tE] [2 - µ]

(c) Longitudinal Strain or axial strain

∈_L = ∈₂ = 1/E[(Pd/4t)- µ(Pd/2t)]

ΔdL/L = ∈_L = [Pd/4tE] [1 - 2µ]

The ratio of Hoop Strain to Longitudinal Strain

∈_H = ∈_L = (circumferential strain)/(longitudinal strain) = {[Pd/4tE] [2 - µ]}{[Pd/4tE] [1 - 2µ]} = [2 - µ]/[1 - 2µ]

Volumetric Strain or Change in the Internal Volume

∈_V = ΔV/V = [Pd/4tE] [5 - 4µ]

Thin Spherical Shells

The figure shows a thin spherical shell of internal diameter ‘d’ and thickness ‘t’ and subjected to an internal fluid pressure ‘P’.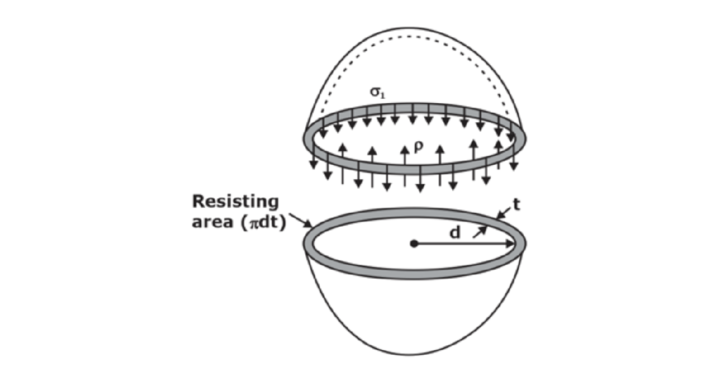

Hoop stress/longitudinal stress

Pressure force by fluid ≤ Resisting force owing to Hoop/Longitudinal stresses P x (π/4)d² ≤ σ.π.d.t Pd/4t ≤ σ For equilibrium, σ = σ_H =σ_L= Pd/4t Hoop stress/longitudinal strain ∈_L = ∈_h = (Pd/4tE)(1- µ)

The volumetric strain of the sphere

∈_L= (3Pd/4tE)(1- µ)

Thick Pressure Vessels

In thick vessels, pressure varies from a maximum at the inner surface to a minimum at the outer surface.
(i) In thick cylinders, hoop stress due to inside pressure is Maximum inside and Minimum outside
(ii) In thick cylinders, longitudinal stress due to inside pressure is constant
(iii) Radial pressure is maximum inside, zero outside, and compressive throughout.

Analysis of Thick Shells using Lame’s Theorem

In this theorem, the material is assumed to be homogeneous and isotropic, and the longitudinal stress is assumed to be constant throughout.

The hoop stress & Radial pressure formula is given below-

Where A & B are Lame’s constant, they are always positive.

By solving these two equations for different boundary conditions, we can find out the values of A & B.

Subjected to only Internal Pressure (p), radial pressure at inside and outside radii is-

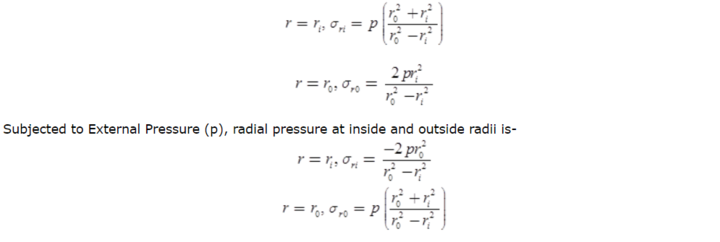
Application of a Thin Cylinder

Thin cylinders are typically employed in applications requiring less pressure force. These cylinders are intended for specific applications. Thin Cylinders are an important part of the GATE ME syllabus. These cylinders are most commonly found in pipes, pressure shells, and boilers. When estimating a mechanical process performed by a narrow cylinder, circumferential stresses are assumed to be constant, and radial stresses are assumed to be negligible.

Key Difference between Thin and Thick Cylinders

The following are the primary distinctions between a thin and a thick cylinder which will help in removing doubts for the upcoming GATE ME exam:

• A thick cylinder has a lower diameter than its wall thickness, whereas a thin cylinder has a larger diameter than its wall thickness.
• A thin cylinder is utilized for low-pressure operations, whereas a thick cylinder is used for high-pressure activities.
• In contrast to a thin cylinder, the circumferential stresses in a thick cylinder are not homogeneous; also, the radial stress is not minor.
• A thin cylinder is utilized in labs and on a small scale. In contrast, a thick cylinder has a considerably broader industrial application: it is used in pipelines and nuclear power plants.