Uniformly Varying Load
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In the designing of Civil Engineering structures, the main concern will be to find out the design parameters which affect the design criteria for those kinds of buildings or structures. Uniformly varying load is one of those parameters which comes into the category of total load criteria. A force that is applied uniformly along the length of support is known as a uniformly varying load. This weight is dispersed throughout the whole length of the support for the least degree of deflection.
In Civil Engineering, and construction works many design parameters need to be considered which include types and different combinations of load, Materials used Strength of subsurface soil, etc. Load acting on structures includes Live load, Dead load, Wind load Earthquake loads, etc. Form of load may be uniformly distributed load, uniformly varying load, point load, etc. Let us check uniformly varying load formula, examples, and more.
Table of content
What is Uniformly Varying Load?
There are many types of loading that occur in the designing of structures. This type of loading may include point load, uniformly distributed load, uniformly varying load, etc. Uniformly varying load is a type of load which consists of zero intensity at one end and linearly varies to the other end.
A uniformly varying load is also called the triangular load which starts with zero intensity at one end of the beam and varies linearly to the other end of the beam. This variation of load comes under the nonuniform distribution of loads over the beam. In such conditions, the reaction on each support will be different, having lower values at the end that consist of zero intensity of loading.
Uniformly Varying Load Formula
Formulas for uniformly varying loads may depend on the parameters which need to be determined and which type of supports are there. It also includes any other type of loading on a beam. Here, formulas for calculating the reactions on supports are given for a simply supported beam having a uniformly varying load.
RA = wL/3 and RB = wL/6
Where RA and RB are the reactions at support A and B respectively.
Uniformly Varying Load Example
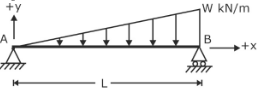
A uniformly varying load can be classified as a load that is distributed along the length of a beam or structure but varies linearly throughout the length of the beam. A most common example of such variation of the load is the variation of thrust force over the retaining wall. Here some examples are given that help to understand the distribution of load over the beam.
Simply supported beam carrying a uniformly varying load from zero at each end to W per unit length at the centre.

Uniformly Varying Load on Cantilever Beam
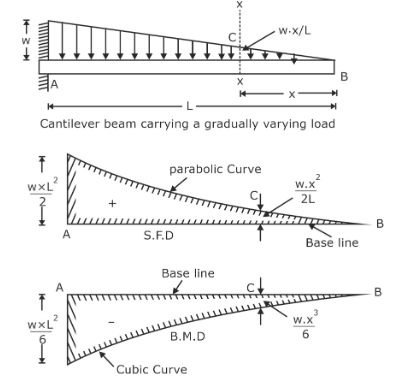
The cantilever beam is a beam that has fixed support at one end and the other end is free. Such types of beams are determinate in nature having zero number of redundant reactions. Uniformly varying load over the cantilever beam may be in the form of zero intensity at the free end or zero intensity at the fixed end. Here a cantilever beam is shown having zero intensity of load at the free end of the cantilever beam.
Cantilever beam with uniformly varying load
Nature of SFD Under Uniformly Varying Load
SFD stands for Shear Force Diagram and it is the variation of shear force along the length of the beam. The nature of the shear force diagram over a beam will depend upon the nature of supports and the variation of loading over the beam. With the help of a shear force diagram, shear force at any section can be determined. Shear force variation for a beam can be expressed as dV/dx=-w.
Shear force variation for a beam is one degree higher than the variation of the loading diagram for the beam. Hence, for the uniformly varying load, the shear force will be the second-degree curve; the as uniformly varying load is a one-degree curve.
SFD and BMD of Uniformly Varying Load
SFD and BMD is the curve that shows the variation of shear force and bending moment respectively along the length of the beam. Shear forces can be stated as a change in bending moment with respect to length along the longitudinal direction of the beam. It can be related as V=dM/dx. The shape of the shear force diagram and bending moment diagram for the cantilever beam subjected to uniformly varying load is of the second-degree and third-degree curves respectively.
Shear force and bending moment diagrams for a cantilever beam carrying a uniformly varying load