- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Impulse and Momentum
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Before diving into the details of Impulse and Momentum, let’s first understand the significant difference between impulse and momentum. The impulse is the change in momentum that occurs when a strong force is applied to an object for a brief period of time. The momentum of the item is determined by the product of its mass and velocity. An object in a collision experiences an impulse equal to the change in momentum.
Impulse and Momentum are important Engineering Mechanics topics commonly asked in various competitive exams. We provide detailed solutions to help you score good weightage of marks on this topic. Go through the Impulse and Momentum study notes for GATE, SSC JE, ESE IES, ISRO, and other Mechanical Engineering exams. In this section, we will go through impulse and momentum in-depth and see how they may be applied to various circumstances using appropriate examples. Before properly understanding the concept of impulse, we must first understand the concept of momentum.
Table of content
What are Impulse and Momentum?
When a powerful force is applied to an item for a short period of time, the impulse causes a change in momentum. The item’s momentum is determined by its mass and velocity. Impulse and Momentum are important parts of the GATE ME syllabus. In a collision, an object experiences an impulse equal to the change in momentum.
Impulse and Momentum GATE Notes
- A change in momentum can be simply called an impulse. The force of interaction might vary with time in a collision between two particles.
- Suppose the force is present for a short amount of time, zero before clock time ti and zero after clock time tf and it has a comparatively high value at maximum.
- The time elapsed for the interaction is approximate, ∆t = tf – ti.
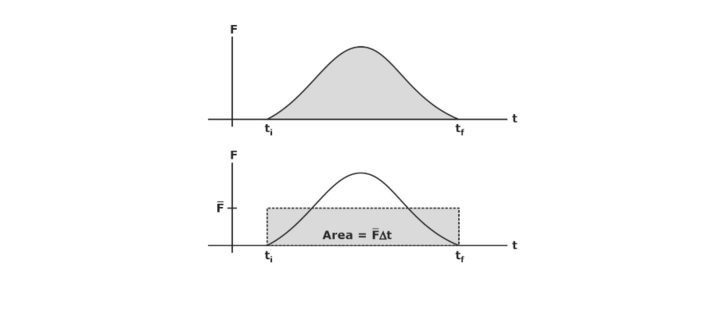
From the figure above, it can be seen that force varies over a relatively short time. The area gives the magnitude of the impulse under the force curve.
- We must integrate, over the elapsed time for the interaction, to find the change in momentum:
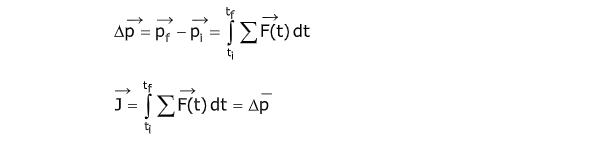
- Change in momentum is known as the impulse and is depicted by the symbol vector J.
- Impulse has the same units and dimensions as momentum and is also a vector.
- The impulse magnitude is equal to the area under the force curve between the two clocked times, that is, over the collision duration.
- The impulse vector’s direction is the same as the direction of the change in the momentum vector.
As per Newton’s Second Law, the net force equals the acceleration times the mass of the object, Substitution of Newton’s Second Law can be done into the equation for impulse,

The difference between the velocities at the starting and ending times is the change in velocities,
Δv= v2-v1
Thus, the formula for impulse becomes,
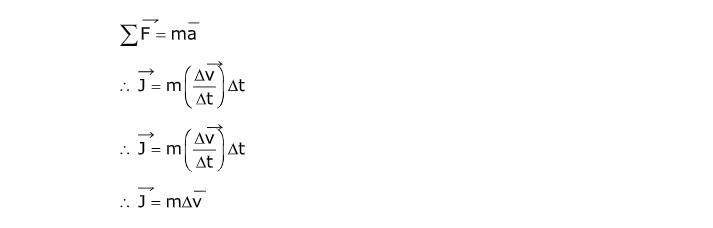
The above equation is called the impulse-momentum theorem. It can also be seen as the change in momentum of an object in a certain time interval equals the impulse of the net force that acts for the particular time interval on the object. With this formula, changes in momentum can be related to the forces that are applied to cause the change. There is a change in momentum resulting from the force applied for a specified time duration.
Momentum
The word momentum is frequently used in sports. A team has momentum when a sports commentator says it, meaning that the team is truly moving forward and will be challenging to stop. Momentum is a physics concept. Any moving object will be challenging to stop. A force must be applied against its motion for a set amount of time to stop such an object. A moving thing has a tougher time stopping the more momentum it possesses. As a result, stopping such an object would take more force, a longer period of time, or both. As the force works on the item for a specific period of time, the object’s velocity changes, and thus the momentum of the object changes.
Download Formulas for GATE Mechanical Engineering – Fluid Mechanics and Machinery
Impulse
One of the reasons impulse is significant and effective is that forces in the real world are not always constant. Forces caused by objects like humans and engines build up over time and vary depending on circumstances. It would be difficult to directly calculate these forces’ overall influence. The product of the average net force acting on an object for a given duration is frequently defined as the impulse.
Impulse and Momentum Formula
Momentum is a vector quantity with the same direction as the object’s velocity. Impulse is the amount of force multiplied by the time it is applied. The direction of the impulse is the same as the direction of the force. Following is the formula for impulse and momentum.
Formula of Momentum
Momentum is a measure of mass in motion: how much mass is involved in how much movement. It is commonly denoted by the sign ‘P.’
P = m.v
Formula of Impulse
The formula for impulse is as follows:
J= F . Δt
Impulse and Momentum SI Unit
The product of mass and velocity gives the item’s momentum, whereas the impulse is the change in momentum when a large force is applied to an object over a brief period of time. The impulse felt by an object in a collision equals the change in momentum. Following are the SI units for impulse and momentum.
SI Unit of Momentum
Momentum is always measured in kg.m/s and is always a vector quantity.
SI Unit of Impulse
The newton second (N.s) is the SI unit of impulse.
Download Formulas for GATE Mechanical Engineering – Strength of Materials
Impulse Momentum Theorem
The Impulse-Momentum theorem assists us in determining the relationship between the two notions. The theorem basically states that the change in momentum of an object is proportional to the amount of impulse applied to it.
Essentially, students should understand that impulse is a measurement of how much momentum varies. We also get an alternative formula here, which is as follows:
→ → →
J = P2 – p1
Where, P1 = initial momentum and P2 = final momentum
Newton’s Second Law
According to Newton’s second law (Fnet = m • a), an object’s acceleration is inversely related to its mass and directly proportionate to the net force exerted on it. Various MSQ-based questions are formulated in the GATE exam on Newton’s Second Law. The following equality is produced when the definition of acceleration (a = change in velocity/time) is applied.
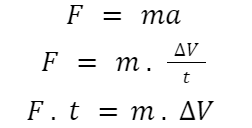
This equation reflects one of two key principles that will be applied in the collision analysis during this unit. To fully understand the equation, it is essential to understand its meaning in words. In other words, the force multiplied by the time equals the mass multiplied by the velocity change. The quantity Force • time is known as an impulse in physics. And, since the quantity m•v represents momentum, the quantity m•Δv must represent momentum change. The equation truly states that
Impulse = Change in Momentum
Conservation of Momentum
During the interaction of two objects, like in a collision, forces may be exerted on each other. The forces the objects exert on each other can be considered a part of a closed or isolated system; in that case, the forces involved are internal forces. If any external force affects the system, it is called external force.
As per Newton’s Third Law, if there are no external forces, the internal forces that act between two objects have opposite directions and equal magnitude. Assume the two objects as A and B; the forces they exert on each other are,
FA on B = – FB on A
- When a collision occurs, these forces act at the same time. Consider the collision to begin at time t1 and end at time t2, which makes the time duration of the collision as Δt, and the object A experiences the impulse equal to,
JA = FB on AΔt - On substituting these impulse equations in place of the forces, we get,
FA on B = – FB on A
∴JB/Δt = JA/Δt
JB = JA
Hence the impulse-momentum equation becomes equivalent to the following:
![]()
- In this equation, PA1 means the momentum of object A at time t1, PA2 means the momentum of object A at time t2, PB1 means the momentum of object B at time t1, and PB2 means the momentum of object B at time t2.
- The equation can be rearranged to put all of the terms for time t1 on one side, and terms for time t2 on the other,
![]()
- Without the presence of any external force, the total momentum of the system remains constant. This is referred to as the conservation of momentum.
- The total momentum labeled as P for any number of objects equals
![]()
Even if the momenta of the individual objects change, the total momentum will remain the same when no external force is acting on the bodies.
Linear Momentum and Its Conservation
A particle of mass m moving with velocity v has a linear momentum which can be defined as the product of mass and velocity. Since linear momentum is the product of a scalar and a vector, therefore it is a vector.
p = mv
- Dimensions of linear momentum are M.L.T–1 and units kg.m.s–1.
- The direction of the momentum vector is identical to that of the velocity vector.
Newton’s second law in terms of linear momentum can be expressed in this way
- The time rate of change of linear momentum of the object (system) is the resultant force on an object (system).
- If the system is isolated, a law regarding the conservation of linear momentum can be formulated.
Instantaneous Impulse
Let us see an example of the instantaneous impulse essential as per the GATE notes:
Example: bat and ball contact
![]()
- The expression can understand the relationship between linear momentum and impulse,
F× t = m (v-u) Where,
F = Force, t = time, m = mass, v = initial velocity, u = final velocity about a fixed point gives the three-dimensional motion of a rigid body attached at a fixed point.


