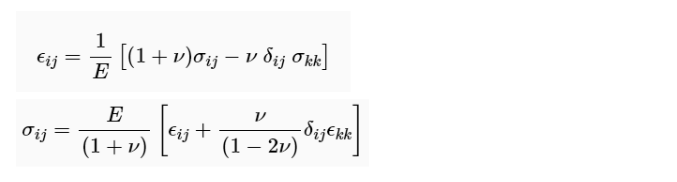- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Difference Between Plane Stress and Plane Strain | Plane Stress vs Plane Strain
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Before we get into the specifics of Plane Stress vs Plane Strain, let’s define stress and strain. Strain is defined as the amount of distortion experienced by the body in the direction of the applied force divided by the body’s initial dimensions The internal resistance provided by the body to the external load per unit cross-sectional area is referred to as stress. Plane stress implies that tension can only exist in-plane, with no out-of-plane stress produced.
Plane Stress vs Plane Strain PDF
Plane-stress analysis employs the analogy of a thin shell; the model is essentially gazing down at this thin shell from above. The shell can be compressed or extended within the plane of analysis, and strain will be formed in the out-of-plane direction due to the applied Poisson’s ratio. Plane strain implies that strain can only exist in-plane, with no out-of-plane strain produced. This is because the boundary condition in the out-of-plane direction is constrained (movement is prevented). There is no strain in the out-of-plane direction since movement is restricted. Instead, stress will be generated due to the fixity of movement. A cross-section of an endlessly long element is equivalent to this. Let’s understand Plane Stress vs Plane Strain detail.
Download Formulas for GATE Mechanical Engineering – Strength of Materials
Table of content
Plane Stress vs Plane Strain
Plane stress is an approximation, but the plane strain is an accurate solution. Plane strain is a specific solution to the entire three-dimensional elasticity equations, whereas plane stress occurs only when the thickness of the laden body approaches zero. Stress, or the force applied to a material, is defined as the force divided by the substance’s cross-sectional area. Both Plane Stress and Plane Strain are important as per the GATE exam. Strain is a material’s deformation or displacement induced by applied stress.
Difference Between Plane Stress and Plane Strain
Plane strain is a precise solution, whereas plane stress is an approximation. In contrast to plane stress, which only manifests when the thickness of the laden body approaches zero, plane strain is a specific solution to the whole set of three-dimensional elasticity equations.
Download Formulas for GATE Mechanical Engineering – Manufacturing Engineering and Materials
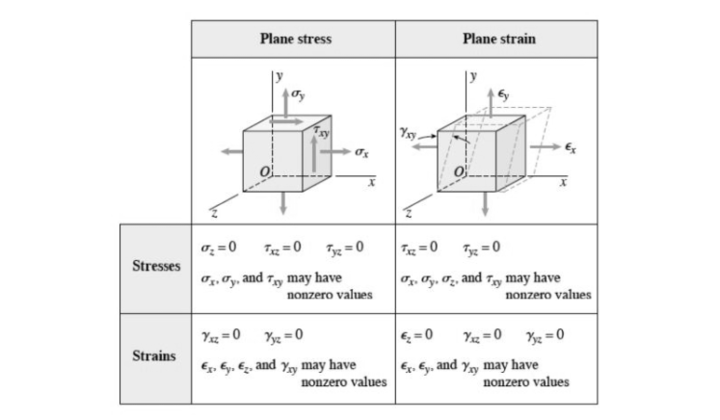
Plane Stress
Plane stress is a state where the normal stress remains zero, and the shear stress in the direction perpendicular to the applied load is assumed to be zero. In planar stress, one of the object’s dimensions is insignificant compared to the other two dimensions. Plane stress is widely used in formulating questions in the GATE ME question paper. In basic terms, a uniform load is given to the object’s thickness, which is substantially smaller than the object’s other two dimensions.
Furthermore, the shear stress caused by the load can be minor since it causes negligible deformations in the object’s thickness. There is insufficient limit material to maintain constant thickness stress:
σZ = σXZ = σYZ = 0
Plane Strain
In simple strain, the object’s thickness is significantly greater than its other two dimensions. Plane strain distorts an object’s dimension in the plane’s perpendicular directions. Plane strain assumptions are useful for modelling real-world components. MSQ-based questions are formulated using the plane strain concept in the GATE question paper. In-plane stresses are created in the same way that they are in a full 3D model, but out-of-plane or z-direction strains are set to zero. It occurs in an object with strong z-direction walls. The formulation only allows for stress reduction in the plane, hence the plane strain:
ZZ= XZ= YZ= 0
Download Formulas for GATE Mechanical Engineering – Machine Design
Hooke’s Law
The interaction of the three normal stresses and strains is the primary influence of plane stress and strain assumptions. Hooke’s law is a very important part of the GATE ME syllabus. To see this, you must be familiar with Hooke’s Law, but only for regular stresses and strains, not shears. Remember that Hooke’s Law can be summed up in a single tensor equation.