- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
What is Parallelogram Law of Forces? Statement, Proof, Formula
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Let’s take a closer look at force before we enter the Parallelogram Law of Forces. A force is an influence that can modify the motion of an object. A force can change the velocity of an object. A push or a pull are two apparent ways to define force. Because it has both magnitude and direction, a force is a vector quantity. It is symbolized by the letter F and measured in newtons (N).
Parallelogram Law of Forces PDF
The parallelogram of forces is a method for solving (or illustrating) the outcomes of two forces applied to an object. The geometry is no longer parallelogrammatic when more than two forces are involved, but the same principles apply. Because forces, being vectors, obey the principles of vector addition, the overall (resultant) force owing to the application of several forces can be calculated geometrically by drawing vector arrows for each force. Let us take a deep look into the concepts associated with the parallelogram law of forces.
Table of content
State Parallelogram Law of Forces
Suppose two vectors acting on a particle simultaneously are represented in magnitude and direction by the two adjacent sides of a parallelogram formed from a point. In that case, their resultant vector is represented in magnitude and direction by the diagonal of the parallelogram drawn from the same point, according to the law of parallelogram of forces.
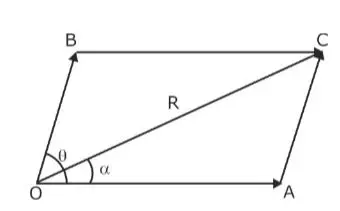
Assume that two vectors, A and B, both inclined at angle θ, are operating on a particle at the same time. Let them be represented by two neighbouring sides, OA and OB, of the parallelogram OACB, drawn from a point O, in magnitude and direction. This law is widely used in solving problems in the GATE exam. According to the parallelogram law of vectors, the resultant vector will be represented by the parallelogram’s diagonal.
- It should be observed that the size of the resultant of two vectors is greatest when they act in the same direction and least when they act in opposing directions.
- It should be noted that when using the parallelogram law of vector addition to obtain the resulting vector of two vectors, the two vectors A and B should either act towards or away from the point.
Parallelogram Law of Forces Formula
Suppose the magnitude and direction of two forces acting at a point are represented by the two adjacent sides of a parallelogram. In that case, the resultant is represented by the diagonal of the parallelogram formed from the same point. Following is the formula for resultant force by using the Parallelogram Law of Forces.
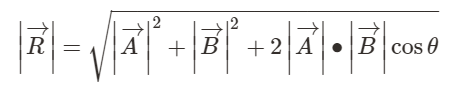
Special Case of Parallelogram Law of Forces
Let us see a few important and special cases of the parallelogram law of forces that will help solve the problems in the GATE question paper.
- Case 1: When two vectors act in the same direction, then θ=0°, cosθ = 1.
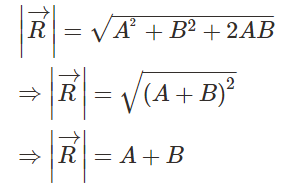
- Case 2: When two vectors act in opposite directions, then θ =180° and cosθ = −1.
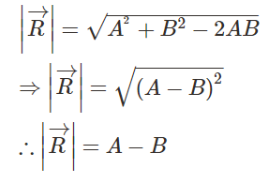
Thus, when two vectors act in different directions, the magnitude of the resulting vector equals the difference between the magnitudes of the two vectors and acts in the direction of the larger vector.
Newton’s Proof of the Parallelogram Law of Forces
Assume two forces act on a particle at the figure’s origin below. Let the lengths of the vectors F1 and F2 reflect the velocities that the two forces may induce in the particle if they were to act for a given duration, and the direction of each represents the direction in which they act. Each force acts separately and will produce its own velocity whether or not the other force acts. The particle has both velocities at the end of the allotted time. According to the previous proof, they are identical to a single velocity, Fnet. According to Newton’s second law, this vector is also a measure of the force that would cause that velocity; hence the two forces are equivalent.

Parallelogram Law Proof
If two vectors acting on a particle at the same time are represented in magnitude and direction by two adjacent sides of a parallelogram drawn from a point, their resultant is represented by the diagonal of the parallelogram drawn from the same point, according to the law of parallelogram of two forces.


Get complete information about the GATE exam pattern, cut-off, and all those related things on the BYJU’S Exam Prep official youtube channel.



