What is Scaling in Computer Graphics?
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Scaling in Computer Graphics is one of the fundamental transformations. Transformation is a process of modifying and re-positioning the existing graphics.
Transformations help change the object’s position, size, orientation, shape, etc. There are three basic rigid transformations: reflections, rotations, and translations. There is a fourth common transformation called dilation. Further, we have discussed scaling in computer graphics, transformation, and a lot more in the upcoming sections.
Table of content
What is Transformation in Computer Graphics?
Transformation in Computer Graphics means a change some graphics into something else by applying rules. In other words, transformation is the change of an object(position and size) after creation. Transformation can be done in 2D as well as 3D.
Transformation plays a vital role in computer graphics, repositioning the graphics on the screen and changing their size or orientation. The different types of basic geometrical transformation are as follows:
- Translation
- Scaling
- Rotation
The derived geometrical transformation is:
- Reflection
- Shearing
2D Scaling in Computer Graphics
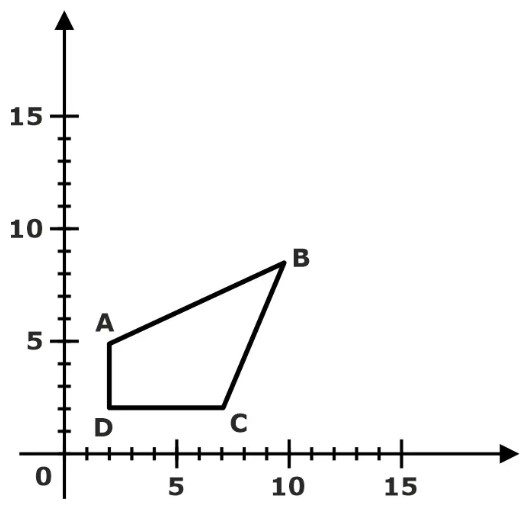
Scaling is the transformation that is used to change the object’s size. The operation is carried out for polygon by multiplying the coordinate value(X, Y) of each vertex with the scaling factors.
Rules for Scaling in Computer Graphics
Scaling is performed about the origin as
If scale > 1, it enlarges the object and moves it away from the origin.
If scale = 1, then it leaves the object the same.
If scale < 1, it shrinks/reduces the object and moves it towards its origin.
What is the Equation for Scaling in Computer Graphics?
Let us suppose the coordinate(X, Y) is the original coordinate before the scaling, Sx, and Sy are the X-axis and Y-axis scaling factors. The new coordinate(X’, Y’) after the scaling is given by the equation:
X’ = X . SX and Y’ = Y . SY
The scaling factor SX and SY scale the object in the X and Y direction, respectively. The above equations may also be represented in matrix form as below:
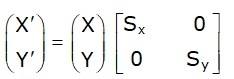
OR
P’ = P . S
The following figure shows the scaling process where S is the scaling matrix.