- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Parallelogram Law of Vectors
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In vector theory, the Parallelogram Law of Vectors is a method for calculating the sum of two vectors. We investigate two vector addition laws: the triangle law of vector addition and the parallelogram law of vector addition. When the vectors to be added create the two adjacent sides of a parallelogram by merging the tails of the two vectors, the parallelogram law of vector addition is employed to add them. The diagonal of the parallelogram then gives the sum of the two vectors.
Parallelogram Law of Vectors PDF
Vector addition can be used to calculate the sum of two vectors, and the parallelogram law of vector addition is a rule that makes calculating the resultant sum vector easier. Let’s take a deep dive at the concepts around the parallelogram law of vectors, along with its formula and derivation.
Download Formulas for GATE Mechanical Engineering – Strength of Materials
Table of content
Parallelogram Law of Vectors
Let us understand the Parallelogram law of vectors with an example. Suppose the magnitude and direction of two vectors acting simultaneously on a particle are represented by the two adjacent sides of a parallelogram drawn from a point. In that case, the resultant is represented in magnitude and direction by the diagonal of that parallelogram formed from that point.
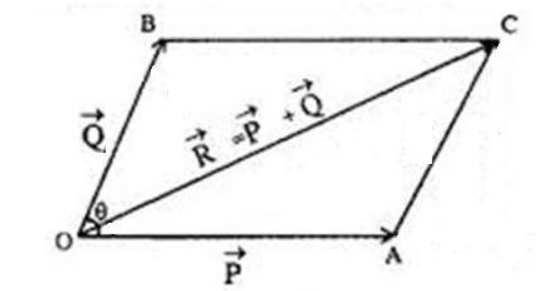
Let two vectors, P and Q operate on a particle O simultaneously. They are represented by the neighboring sides OA and OB of a parallelogram OACB formed from a point O in magnitude and direction. The diagonal OC running across O will thus indicate the size and direction of the consequent R. Parallelogram law of vectors can be used for solving challenging problems in the GATE exam.
If a body of unknown weight (say S) is suspended from the middle hanger of Gravesand’s apparatus, and balancing weights P and Q are strung from the other two hangers, then
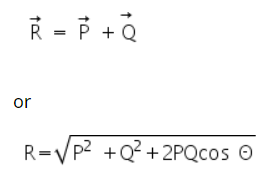
Formula of the Parallelogram Law of Vectors
Consider two vectors, P and Q separated by an angle θ. The vector R, the resultant sum vector of the parallelogram law of vector addition, gives the sum of vectors P and Q. The formulas for the magnitude and direction of the resulting vector R, if it forms an angle ϕ with the vector P, are:
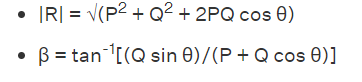
Download Formulas for GATE Mechanical Engineering – Fluid Mechanics and Machinery
Derivation of Parallelogram Law of Vectors
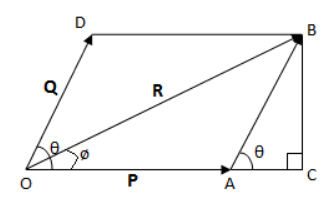
Let P and Q be two vectors acting simultaneously at a point and represented in magnitude and direction by two adjacent sides OA and OD of the parallelogram OABD seen in the figure.
Let θ the angle formed by P and Q, and R be the resulting vector. The resultant of P and Q is therefore represented by diagonal OB, according to the parallelogram law of vector addition.
Magnitude of Resultant
Let us see the formula that can be used to find the magnitude of the resultant thus found by using the parallelogram law of vectors. Magnitude found out by using the parallelogram law of vectors can be used in solving GATE question papers.

Download Formulas for GATE Mechanical Engineering – Thermodynamics
Direction of Resultant
Let ø be the angle formed by the resultant R with P. Then, From the OBC triangle given in the figure shown above.

Get complete information about the GATE exam pattern, cut-off, and all those related things on the BYJU’S Exam Prep official youtube channel.



