Eccentric Loading

What is Eccentric Loading?

If a load’s line of action travels through a point other than the column’s axis and away from the axis, the load is said to be eccentric. An eccentric load, to put it simply, acts away from the axis of the column. Eccentricity is denoted by the letter e and is defined as the separation between the column’s axis and the eccentric load’s line of action. When an entire column section is subjected to eccentric pressure, both direct and bending stress is generated.

Now assume one column, as shown in the image, that is fixed at one end and has one weight P applied to the other end of the column at a distance e from the column’s axis. Simply put, the column will experience the eccentric load previously discussed, with the load’s line of action being e distances from the column’s axis.

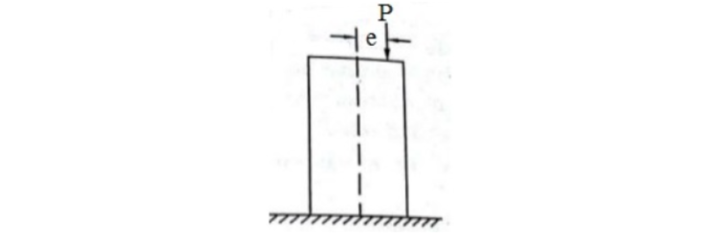
We have the following information from the above figure

P = Eccentric load, which is acting at a distance e from the axis of the column

A= Area of a cross-section of the given column = b x d, (For rectangular cross-section)

b= width of the given column’s cross-section

d= height or depth of the cross-section of the given column

I is the area moment of inertia of the column rectangular section across the axis YY = db3/12

M = Moment formed by the load P = P x e

e = eccentricity of the load P

As previously stated, only direct stress is produced when a body is subjected to an axial tensile or axial compressive load. Similarly, only bending stress is produced when a body is subjected to a bending moment. Consider a body subjected to axial tensile or compressive loads and bending moments; in this case, direct stress and bending stress will be produced. In the event of eccentric loading, the column will experience both direct and bending stress. Because load P is acting downward on the column and the other end of the column is fixed, direct compressive stress will develop in the column.

Direct Stress

Axial applied compressive load/area of cross-section of the given column = direct compressive stress developed in the column.

σ_d = P/ A

σ_d = P/ (b x d)

Unit of Direct compressive stress = N/mm²

Bending Stress

Because of the eccentric load P acting at e distance from the axis of the column, one bending moment will be created, and that bending moment will be stated as M = P x e.

Bending stress will be created in the column due to this bending moment. Remember the concept of bending stress, and we’ll write the expression for the bending stress that develops in the body here.

Eccentric Loading Examples

Different types of eccentric loading cause uneven structural stress distribution. This article goes over eccentric loading on a column and beam.

Eccentric Loading of a Column

Axial loads parallel to the column’s axis are frequently designed into columns. However, in other applications, columns are loaded off-center. As a result, the structure is subjected to increased bending stress, which is more dangerous than compressive or tensile stress. The eccentric loading on a pin-pin column and the associated deflection and tension are simplified in this section. The midsection of a column subjected to an eccentric force under these end conditions experiences the maximum deflection. where x = (L / 2). As a result of this, the maximum deflection is as follows:

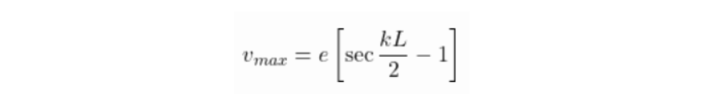
Column Stress

Consequently, the column will experience direct and bending stress, as previously mentioned. The maximum resultant stress (σ_max) will occur where the bending is greatest since only the bending stress varies throughout the column and the direct load is constant. which are v_max and M_max. the following is the expression for maximum resultant stress:

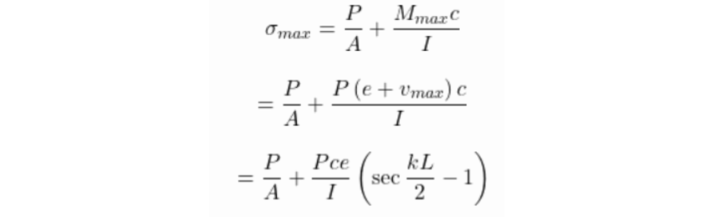
Applications of Eccentric Loading

Eccentric loading is a common type of loading that is encountered in many engineering applications. Some examples of applications where eccentric loading may be important to consider include the following:

• Structural engineering: Eccentric loading is often encountered in the design of structures such as bridges, buildings, and other types of infrastructure. In these cases, it is important to consider the effects of eccentric loading on the structural integrity and stability of the structure.
• Mechanical engineering: Eccentric loading is also commonly encountered in the design of mechanical components and systems, such as gears, bearings, and other rotating machinery types. In these cases, it is important to consider the effects of eccentric loading on the components’ strength, stiffness, and durability.
• Aerospace engineering: Eccentric loading is also encountered in aircraft design and other aerospace systems. In these cases, it is important to consider the effects of eccentric loading on the structural integrity and performance of the aircraft.
• Civil engineering: Eccentric loading is also encountered in the design of civil engineering structures such as roads, tunnels, and other types of infrastructure. In these cases, it is important to consider the effects of eccentric loading on the structural integrity and performance of the structures.
• Material science: Eccentric loading is also used to study materials’ strength, stiffness, and mechanical properties. This can involve performing laboratory tests to simulate eccentric loading conditions and studying the behavior of materials under these conditions.

Important GATE Notes
Steel	Zero Force Member In A Truss
Difference between Machine and Mechanism	Transverse Loading
Geometric Design Of Highways	Void Pointers in C
Macaulay’s Method	Impact Load
Impulse An Momentum	Uniformly Varying Load

Get complete information about the GATE exam pattern, cut-off, and all those related things on the BYJUS Exam Prep official youtube channel.