- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Combined Stress
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The combined stress consists of the bending stress and shear stress generated due to the external load on the beam or column cross-section. Combined stress is one of the important topics of the GATE CE and other competitive exams. These stresses are induced in the material due to transverse loading over the beam.
Combined Stress PDF
The effect of combined stresses in the beam results in distortion of a particular beam section. The beam section’s combined stresses analysis has been carried out based on certain assumptions. These combined stress assumptions are discussed in this article with detailed information.
Table of content
What is the Combined Stress?
Combined stress is the effect of transverse loading over the cross-section of a beam. It consists of the bending stress and the shear stress due to the external loading. Combined stress is the combination of direct stresses, bending stresses and shear stresses. These stresses can be defined as below.
- Direct Stress ⇒ σd = P/A, where P = axial thrust and A = area of cross-section
- Bending Stress ⇒ σb = My/l, where M = bending moment, y- a fibre distance from the neutral axis, and I = moment of inertia.
- Shear stresses ⇒ Τ = Tr/J, where T = torque, r = radius of the shaft, and J = polar moment of inertia.
Combined Stress due to these stresses can be explained as follows
-
Equivalent Torsional Moment
The equivalent torsional moment is defined as the torsional moment, which, when acting alone, will produce the same torsional shear stress in the shaft as under the combined action of bending moment (Mb) and torsional moment (Mt)
⇒ [(Mb)2 + (Mt)2]0.5
-
Equivalent Bending Moment
The equivalent Bending moment is defined as the bending moment, which, when acting alone, will produce the same bending stresses (tensile and compressive) in the shaft as under the combined action of bending moment (Mb) and torsional moment (Mt)
⇒ Mb + [(Mb)2 + (Mt)2]0.5
-
Stress due to Combined Direct and Bending Load
Suppose a beam is under direct compressive and bending load, as shown in the diagram.
where
- A = Area,
- y = distance of extreme fibre from the Neutral axis and
- I = moment of Inertia

Direct compressive stress σ = F/A
Bending stress will vary linearly from centre to extreme fibre σb = My/I
so, total stress at upper fibre = Direct compressive stress+ tensile stress due to a bending load
⇒(-σ)+σb
⇒ -F/A + My/I
Same for lower extreme fiber= Direct compressive stress+ Compressive stress due to bending load
⇒(-σ)+(-σb)
⇒ -F/A – My/I
Bending Stress in Beam
Bending stress and shear stress distribution are classified into two groups. When the beam is bent by downward transverse loads, the fibres near the top contract in length, whereas those near the bottom of the beam extend. Somewhere in between, there will be a plane where the fibres do not change length. This is called the neutral surface. Such a deformation of the beam is called bending.
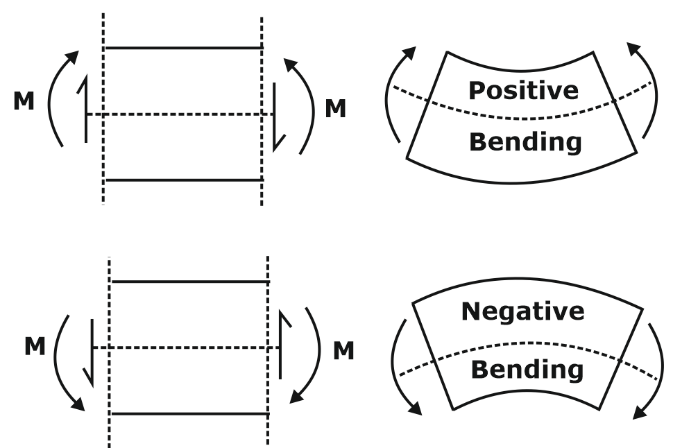
Bending Moment in Beam
Bending moments in beams can occur due to various reasons. Some of the causes of bending moments are explained below.
- Transverse or lateral loads: Forces or moments having their vectors perpendicular to the axis of the bar.
- Classification of structural members
- Axially loaded bars: Supports forces having their vectors directed along the axis of the bar.
- Bar in tension: Supports torques having their moment vectors directed along the axis.
- Beams
- Subjected to lateral loads: Beams undergo bending (flexure) because of lateral loads.
When the beam is subjected to a bending moment or bent, there is induced longitudinal or bending stress in the cross-section.
Equation of Pure Bending
The equation of pure bending relates the bending stress at a distance from the neutral axis of the cross-section, its modulus of rigidity, the radius of curvature and moment of inertia, etc. This equation has been established by considering certain assumptions for the beam’s cross-section. These assumptions are as follows:
Assumptions
- The material of the beam is homogeneous and isotropic.
- Young’s Modulus of Elasticity value is the same in tension and compression.
- The transverse sections, which were plane before bending, remain plane after bending also.
- The beam is initially straight, and all longitudinal filaments bend into circular arcs with a common centre of curvature.
- The radius of curvature is large compared to the dimensions of the cross-section.
- Each beam layer is free to expand or contract, independent of the layer above or below.
The Flexural (or bending) equation can be written as follows.
σ/y = E/R = M/I
Modulus of Section
Elastic section modulus is defined as Z = I / y, where I is the second moment of area and y is the distance from the neutral axis to any given fibre. Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. For the equilibrium of the section, the moment of resistance must be equal to the bending moment M.
It can be written as M = Mr = EI/R (as E/R = M/I)
- For the rectangular section, I = bd3/12. So Modulus of section (z) = bd2/6
- For the circular section, I = πd4/64. So Modulus of section (z) = πd3/32
Beams of Uniform Strength
Generally, beams have a uniform cross-section throughout their length. When a beam is loaded, there is a variation in bending moment from section to section along the length. The stress in extreme outer fibre (top and bottom) also varies from section to section along their length. The extreme fibres can be loaded to the maximum capacity of permissible stress (say σmax), but they are loaded to less capacity. Hence, there is a considerable waste of materials in beams of uniform cross-section.
The beam is said to be in uniform strength if the maximum bending stress is constant across the varying section along its length. When a beam is suitably designed such that the extreme fibres are loaded to the maximum permissible stress σmax by varying the cross-section, it will be known as a beam of uniform strength.
Shear Stress in Beams
In the maximum shear stress theory, the presence of shear and the distortion of plane sections were neglected because their effect on bending stress is not of practical importance. But, it is important to consider the shear stresses for their own importance. Here, only the shearing stresses in the transverse planes parallel to the shearing force and the complimentary shear stresses in the longitudinal planes parallel to the axis of the beam are considered. It is important to know that thermal stresses can also be generated depending on the implied load which is usually neglected.
Shear Stress Distribution Over a Rectangular Beam Section
Shear stress distribution over a rectangular cross-section follows parabolic distribution and can be represented below.
Shearing stress at a section located at a distance y from the beam’s neutral axis.
τ = F(Ay‾)/IZ
Where,
- V = Shearing force
- (Ay‾) = First moment of area
τ = VQ/Ib
Shear Stress in Rectangular Beam
Shear stress at the longitudinal layer having y distance from the neutral axis.
τmax = 1.5 V/A ⇒ τmax = 1.5 τavg
Shear Stress in Circular Beam
The Centre of gravity of a semi-circle lies at a distance from the centre or baseline. As it is symmetrical above the neutral axis, hence at the neutral axis, shear stress will be maximum and when this normal stress is maximum or minimum, it is called the principal stress.
τmax = 4V/3A ⇒ τmax = 1.33 τavg
Shear Stress in Triangular Section
In a triangular cross-section ⇒ τmax = 1.5 τavg
For more information about the bending, shear and combined stresses in the structural member, you can refer to the following video on the Byju Exam Prep’s official youtube channel.
If you are preparing for ESE/ GATE or other PSU Exams (Mechanical Engineering), then avail Online Classroom Program for ESE and GATE ME.



