Direct Stress
By BYJU'S Exam Prep
Updated on: September 25th, 2023

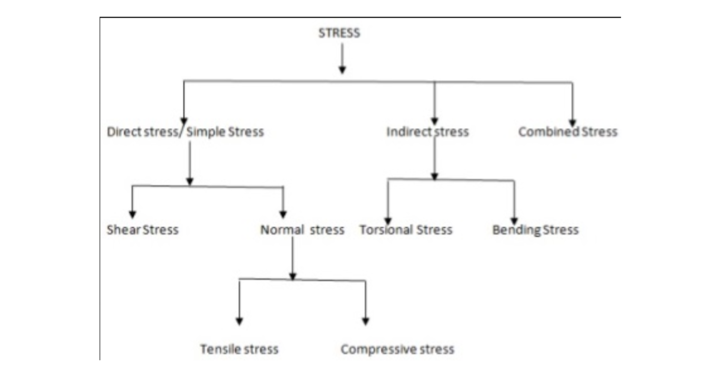
Direct stress is the stress which is induced due to the applied load when it is perpendicular to the body or structure. When the load is directly applied by tangential force, then shear force is developed in the body or structure. Depending upon the type of loading and cross-section of structure and position of load, the direct stress is divided into several types.
This article elaborates on direct stress, the type of load with respect to variation of stress when it acts on the center of gravity, and the occurrence of eccentricity when the load is not acting upon the center of gravity. The method of finding minimum stress and maximum stress using an example of a column. Let us understand direct stress.
Table of content
What is Direct Stress?
The Stresses which are acting normal in the plane of the body are called normal or direct stresses. Stresses are called normal when acting perpendicular to the plane of the body.
Direct stress is the stress developed due to force applied which is parallel or collinear to the axis of the component. Examples of this type of stress are tensile stress, compressive stress, shear stress, and thermal stress.
Differentiate Between Direct Stress and Bending Stress
Direct tensile and compressive stress is set up due to load applied parallel to the length of the object and direct shear stress is set up in the section which is parallel to the line of action of the shear load. But bending stress is set up due to load at right angles to the length of the object subjected to bending. So simple stress is subdivided into 3 types of stress.
Shear Stress
When shear force is applied along the surface, in opposition to an offset force acting in the opposite direction. Shear stress occurs when a shear force is acting on a body. Each of these stresses affects an object in different ways and is caused by the internal forces acting on the object. The direct stress is produced by bending moments or by the bending action of shear loads, while the shear stresses are due to shear and/or torsion of a closed section beam or shear of an open section beam.
Stress due to Concentric Loading
Let us consider a column in which is one end fixed and another end having when the load acts at the center of gravity of the cross-section. In simple terms, we can say that a column is subjected to compressive load. So, direct compressive stress developed only in the body, and the intensity of this direct compressive stress will be uniform across the cross-section of the column in the below figure.
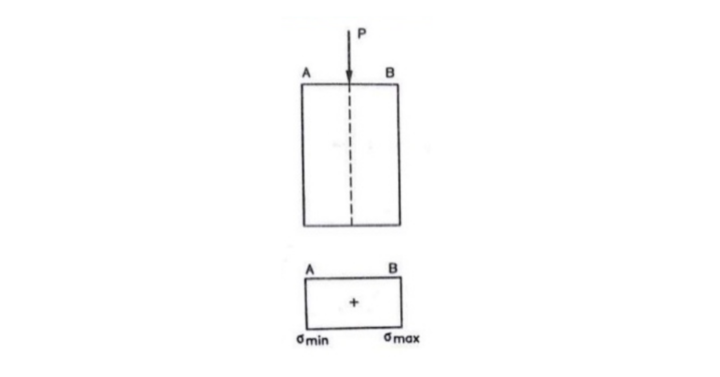
Direct compressive stress developed in the column,
σd= (Axial applied compressive load/ Area of cross-section) of the given column
σd = P/A
σd = P/(b.d)
Where,
P= Direct compressive load
A= Area of cross section = b.d ( for rectangular cross-section)
Unit of Direct compressive stress (σd ) = N/mm2
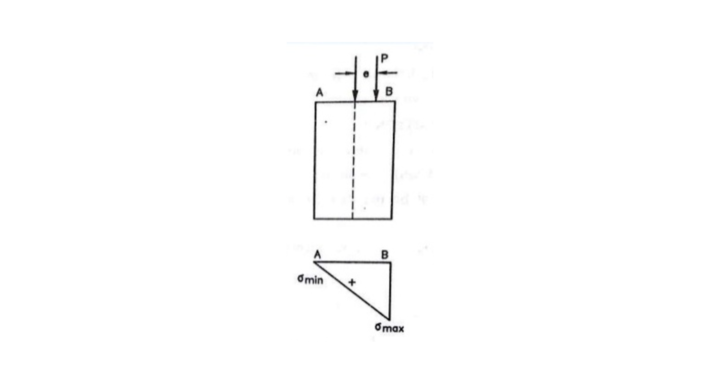
Stress due to Eccentric Loading
When an eccentric load is acting on a column, it produces direct stress as well as bending stress on one side of the neutral axis there is maximum stress and on another side, there is minimum stress. When the bending stress is less than direct stress, the resultant stress will be compressive. If bending stress is equal to the direct stress, there will be tensile stress on one side.
Bending stress, σb=M/(I/y)
M= Bending moment
I= moment of inertia in mm
y = vertical distance of a point away from the neutral axis
I/y = Z = section modulus
Maximum Stress and Minimum Stress
When a column is subjected to eccentric loading, the edge of the column towards the eccentricity is subjected to maximum stress at one end and another end is subjected to minimum stress. Hence, the Maximum stress will be,
σmax= Direct stress + Bending stress
σmax=σd+σb
σmax= P/A + M/Z
Minimum stress,
σmin= Direct stress + Bending stress
σmin=σd– σb
σmin= P/A – M/Z


