- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Elastic Constants: Definition, Formula [Gate Notes]
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Elastic constants are the parameters used to understand an elastic body’s behaviour. Elastic constants are the dimensional constants that establish the relation between strain and stress in a body.
When an elastic body is subjected to a deforming force, in such a case, deformation of the body can be found by using elastic constants. In this article, we will discuss various elastic constants and the relation between different elastic constants.
Table of content
What are Elastic Constants?
Elastic constants are the constants which describe the mechanical response of an elastic material when it is subjected to different kinds of loads. Based on the type of stress and strain, Elastic constants can be classified into 4 types. These Elastic constants are mentioned below.
- Young’s Modulus of elasticity (E)
- Bulk Modulus (K)
- Modulus of rigidity (G)
- Poisson’s ratio (μ)
Young’s Modulus of Elasticity (E)
Young’s modulus of elasticity is an elastic constant that is defined as the ratio of Longitudinal stress to longitudinal strain. When an axial load P is applied along the bar’s longitudinal axis, the bar’s length will be increased in the direction of the applied load, and stress (σ) is induced in the bar.
σ= P/A
According to Hooke’s law, longitudinal stress is directly proportional to longitudinal strain.
Hence,σ∝ε
So, σ=Eε
E= σ/ε
Formulas for GATE Mechanical Engineering – Machine Design
Bulk Modulus (K)
The bulk modulus of elasticity is an elastic constant showing a material’s incompressibility. When a body is subjected to three mutually perpendicular stresses of equal intensity (σ). Then the ratio of direct stress (σ) to the corresponding volumetric strain (ϵv) is defined as the bulk modulus (K) for the material of the body.
Which is generally denoted as ‘K’. Thus,
K = Direct Stress/Volumetric Strain= σ/εv
Volumetric strain: Volumetric strain is defined as the ratio of change in volume of an elastic body to its initial volume. For an equally stressed body in all three mutually perpendicular directions,
Volumetric strain = εv=ΔV/V=εx+εy+εz
Formulas for GATE Mechanical Engineering – Fluid Mechanics and Machinery
Modulus of Rigidity (G)
Modulus of Rigidity is an elastic constant that measures a deformable body’s rigidity.
The shear modulus or modulus of rigidity expresses the relation between shear stress and shear strain. Modulus of rigidity can be defined as the ratio of shear stress to shear strain.
G=Τ/φ
Shear strain (φ): Shear strain is defined as the angular deformation of the body when it is subjected to shear stress.
Poisson’s ratio (μ)
Poisson’s ratio is an elastic constant which is defined as the ratio of lateral strain to longitudinal strain. Poisson’s ratio is a unitless quantity, and it is generally denoted as μ or 1/m.
Poisson’s ratio = -Lateral Strain/Longitudinal Strain
Poisson’s Ratio values for different materials:
|
Material |
Poisson’s ratio (μ) |
|
Cork |
0 |
|
Concrete |
0.1 – 0.2 |
|
Metals |
1/4 to 1/3 |
|
Rubber, Clay, Paraffin |
0.5→ Behaves like a perfectly elastic material |
Relation Between Different Elastic Constants
Among these four Elastic constants, three elastic constants can be related to each other.
These relations can be expressed below.
- E=2G(1+μ)
- E=3K(1-2μ)
- E=9KG/(3K+G)
Some Important Facts about Elastic Constants
The value of any Elastic constants should be ≥ 0.
E, K, G > 0
µ ≥ 0 [because, µcork = 0]
So, for K to be positive, 1 – 2µ ≥ 0 ⇒µ ≤ 1/2
Hence for any engineered material, 0 ≤ µ ≤1/2
| µ | G | K | |
| Minimum Limit | 0 | E/2 | E/3 |
| Maximum Limit | 1/2 | E/3 | ∞ |
Hence, we can say that
- E/2≤G≤E/3 and E/3≤K≤∞
- Asµ↓⇒G↓and K↑
- G≤E
Materials based on Elastic Properties
Materials based on Elastic properties can be categorized as follows.
Homogeneous material
Homogeneous materials are those materials that have similar elastic properties in any of the directions at any point.
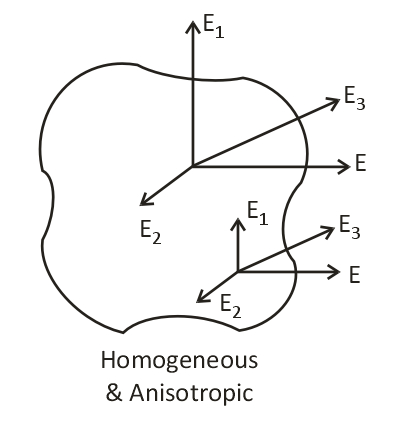
Anisotropic Material
When a material exhibits different elastic properties in every direction at every point, then the material is known as Isotropic Material.
Fig. Anisotropic material

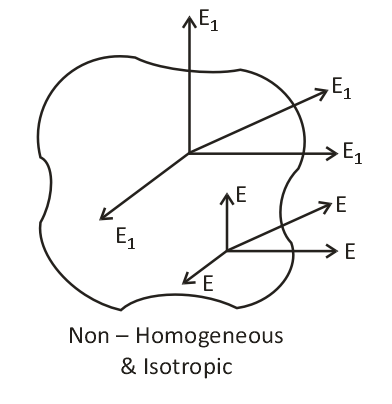
Isotropic Material
When a material exhibits the Same elastic properties in any direction at a given point, then the material is known as Isotropic Material.
For complete information about the elastic constants, you can refer to the following video on Byju Exam Prep’s official youtube channel.
Orthotropic Material
When a material exhibits the Same elastic properties at the only orthogonal direction at a given point, then the material is known as Orthotropic Material.
The Independent elastic constant is the constant which is required to define the stress and strain relationships for a particular type of material. Here the number of independent elastic constants for some materials is given.
|
Type of Material |
No. of Independent Elastic Constant |
|
Isotropic |
2 |
|
Orthotropic |
9 |
|
Anisotropic |
21 |
![Elastic Constants: Definition, Formula [Gate Notes]](https://gs-post-images.grdp.co/2020/3/telegram_png30-1-img1585473029191-76.png-rs-high-webp.png) Daily free APP and Youtube classes, Engineering Jobs, Free PDF & much more, Join our Telegram Group Join Now.
Daily free APP and Youtube classes, Engineering Jobs, Free PDF & much more, Join our Telegram Group Join Now.

