- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Area Moment of Inertia: Definition, Formula, Theorem
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Before diving into the Area Moment of Inertia details, let’s first understand the moment of inertia. The moment of inertia is defined as the quantity expressed by the body resisting angular acceleration, which is the sum of the product of each particle’s mass and its square of the distance from the axis of rotation. In simpler terms, it is a quantity determining the torque required for a certain angular acceleration in a rotational axis. The angular mass or rotational inertia are other names for the moment of inertia. kg-m2 is the SI unit for a moment of inertia.
The second moment of area, also known as the quadratic moment of area or the area moment of inertia, is a geometrical feature of an area that reflects how its points are distributed concerning an arbitrary axis. The second moment of area is commonly indicated by an I (for an axis in the plane of the area) or a J. (for an axis perpendicular to the plane). It is calculated in both circumstances using a multiple integral over the object in the issue. It has a length of L to the fourth power. In detail, let’s take a deep dive into concepts related to area moment of inertia.
Download Formulas for GATE Mechanical Engineering – Strength of Materials
Table of content
Area Moment of Inertia
The area moment of inertia, also known as the second area moment or the 2nd moment of area, is a feature of a two-dimensional plane form that illustrates how its points are distributed in the cross-sectional plane along an arbitrary axis. This property describes the deflection of a plane shape under a load. The area moment of inertia is essential for the GATE exam as MCQ-based questions can be seen in the exam.
For an axis in a plane, the area moment of inertia is commonly indicated by the symbol I. When the axis is perpendicular to the plane, it is also designated as J. The dimension unit of the second area moment is L4 (length to the power of four). The International System of Units unit of measurement is the meter to the power of four, or m4. It can be inches to the fourth power, in4 if we use the Imperial System of Units.
This concept will frequently appear in the field of engineering. In this context, the area moment of inertia is believed to measure a beam’s flexural stiffness. It is a significant feature used to calculate a beam’s deflection or measure its resistance to bending. We’ll look at two examples here.
- First, the planar second moment of the area where the force sits perpendicular to the neutral axis can characterize or define a beam’s bending resistance.
- Second, when the applied moment is parallel to the beam’s cross-section, the polar second moment of the area can be employed to calculate its resistance. It is essentially the beam’s resistance to torsion.
Download Formulas for GATE Mechanical Engineering – Manufacturing Engineering and Materials
Area Moment of Inertia Formulas
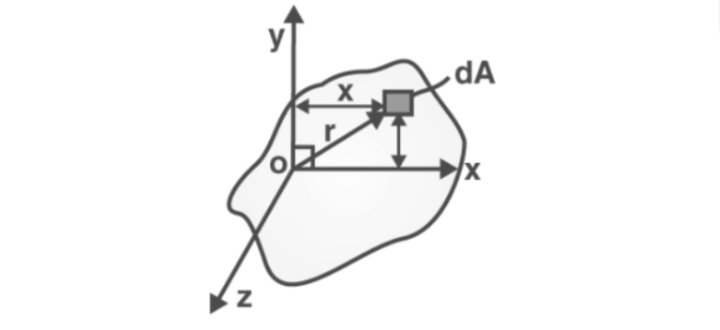
The area moment of inertia formulas can be used to formulate the MSQ-based questions carrying marks scheduled as per the GATE exam pattern. When we consider the area moment of inertia for the x-axis, we get;
Ix = Ixx = ∫y2dxdy
Meanwhile, the area’s product moment is described by
Ixy = ∫xy dx dy
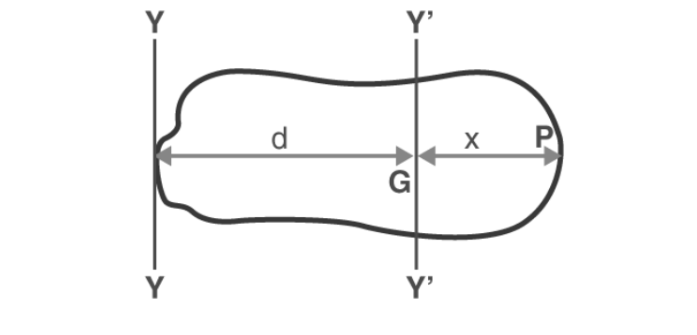
Parallel Axis Theorem
The parallel axis theorem is an essential part of the GATE ME syllabus. A body’s moment of inertia about any axis is equal to the sum of its moment of inertia about a parallel axis passing through its center of mass, the product of its mass, and the square of the distance between the two lines.
I = Ig = Md2
Where:
- M = Mass of the body
- D = the perpendicular distance between the two lines
Perpendicular Axis Theorem
The moment of inertia about a perpendicular axis for a planar body is the sum of the moments of inertia about two perpendicular axes coincident with this perpendicular axis. It sits on the plane of the body. The expression specifies it.
Iz = Ix + Iy
Download Formulas for GATE Mechanical Engineering – TOM & Vibrations
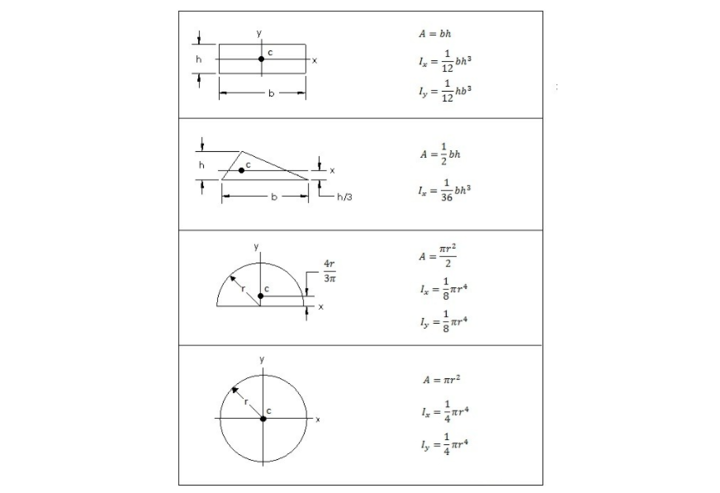
Area Moments of Inertia for Some Common Shapes
The following is a list of some form’s second moments of area. The second moment of area, also known as the area moment of inertia, is a geometrical feature of an area that represents the distribution of its points concerning an arbitrary axis.
If you are preparing for GATE and ESE, avail Online Classroom Program to get unlimited access to all the live structured courses and mock tests from the following link:



