- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Laminar and Turbulent Flow
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Laminar and turbulent flow is the flow characteristics classified based on the Reynolds number of the flow. Reynolds number is a nondimensional number defined as the ratio of inertia force to the viscous force acting on the fluid element. The following article also covers the difference between the laminar and turbulent flow.
Laminar and Turbulent Flow PDF
Laminar and Turbulent Flow is one of the important topics of Fluid Mechanics in Mechanical Engineering, especially if you are preparing for the GATE exam. The article includes fundamental notes on the “Laminar and Turbulent Flow”.
Table of content
-
1.
What are Laminar and Turbulent Flow?
-
2.
Different Correction Factors
-
3.
Turbulent Flow Characteristics
-
4.
Difference Between Laminar and Turbulent Flow
-
5.
Average Velocity and Fluctuating Velocity in Turbulent Flow
-
6.
Reynolds Expression for Turbulent Shear Stress
-
7.
Velocity Distribution in Turbulent Flow
What are Laminar and Turbulent Flow?
Laminar and turbulent flow are the flow conditions described based on the Reynolds number of the flow. The characteristics of the Laminar and Turbulent flow can be expressed below.
Laminar Flow and Turbulent Flow
- Laminar flow occurs in the form of lamina or layers with no intermixing between the layers.
- Laminar flow is also referred to as streamlined or viscous flow.
- In the case of turbulent flow, fluid particles are intermixed.
Reynold’s Number
The dimensionless Reynolds number plays a prominent role in foreseeing the patterns in a fluid’s behaviour. It is referred to as Re and is used to determine whether the fluid flow is laminar or turbulent.
Reynold’s no, Re = ρVD/μ = VD/ν
V= mean velocity of flow through a pipe
D = Characteristic length of the geometry
μ = dynamic viscosity of the liquid (N–s /m2)
ν = Kinematic viscosity of the liquid (m2/s)
Characteristic length (D) can be expressed as 4Ac/P
Where,
- Ac = Cross–section area of the pipe
- P = Perimeter of the pipe
Reynolds number for pipe and plate
|
Pipe |
Plate |
|
Re < 2000 laminar 2000 < Re < 4000 Transient Re > 4000 turbulent |
Re < 5 × 105 Laminar Re > 5 × 105 turbulent [transient is small, so neglected] |
Laminar Flow in a Pipe
In the pipe, the flow may be laminar, turbulent or transition depending upon the Reynolds number of the flow. Reynolds number of the flow in pipes governs by the velocity of the flow, the diameter of the pipe and the dynamic viscosity of the flowing fluid. The pipes’ shear stress and velocity distribution can be formulated with the following expression.
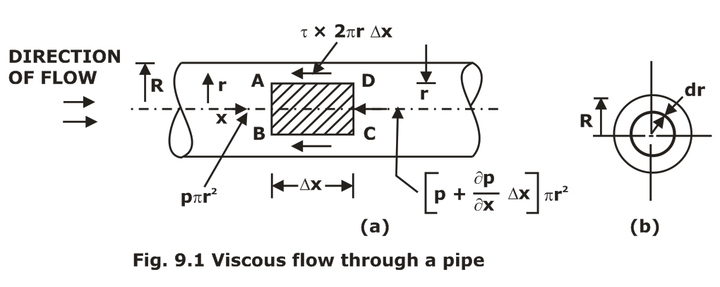
The force analysis on the fluid element can be expressed as follows:
(a). The pressure force, P×πR2 on face AB.
(b). The pressure force on the face CD = [p + (∂P/∂x)Δx ]πr2
(c). The shear force, τ × 2πr∆x, on the fluid element. As there is no acceleration hence:
Net force in the direction of the flow =0
ΣFx = 0 results in
τ = -(∂P/∂x)×(r/2) and τmax at r=R ⇒ -(∂P/∂x)×(r/2)
As pressure variation ∂P/∂x across the section is constant, the shear stress τ varies linearly with the radius r; the variation is shown in the following figure.
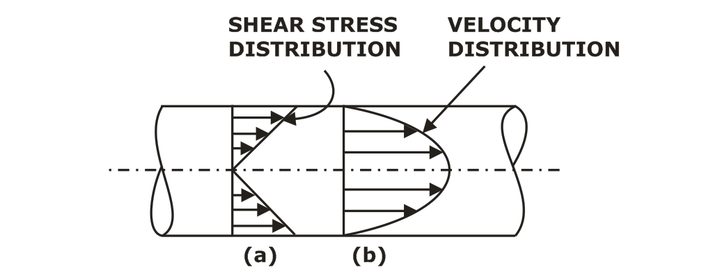
The Ratio of Maximum Velocity to the Average Velocity
Thus, the Average velocity for Laminar flow through a pipe is half the maximum velocity of the fluid at the centre of the pipe.
Umax = -(1/4μ)(∂P/∂x)×R2
Uavg = -(1/8μ)(∂P/∂x)×R2
So, the ratio of maximum to average velocity is 2.
Pressure Variation in Laminar Flow Through a Pipe of Length L
Uavg = (-1/8μ)(∂P/∂x)R2 ⇒ -∂P = 8μuavg∂x/R2
On integrating the above equation on both sides
-ΔP = 8μuavgL/R2 ⇒ P1 – P2 = 32μuavgL/D2
Head loss in Laminar flow through a pipe over length L
(P1 – P2)/ρg = hf ⇒ P1 – P2 = ρghf
P1 – P2 = 32μuavgL/D2 ⇒ hf = 32μuavgL/ρgD2
The above equation is the Hagen Poiseuille Equation.
As we know,
hf = fLu2avg/2gd and hf = 32μuavgL/ρgD2
Thus,
fLu2avg/2gd = 32μuavgL/ρgD2
f= 64/(ρuD/μ) = 64/Re where f is the friction factor
f’ = f/4 = 16/Re where f’ is the friction coefficient
Radial distance from the pipe axis at which the velocity equals the average velocity
Uavg = -(1/8μ)(∂P/∂x)×R2
u = -(1/4μ)(∂P/∂x)×(R2 – r2)
-(1/8μ)(∂P/∂x)×R2 = -(1/4μ)(∂P/∂x)×(R2 – r2)
⇒ r = R/√2 ⇒ r = 0.707 R
Laminar Flow Between Two Fixed Parallel Plates
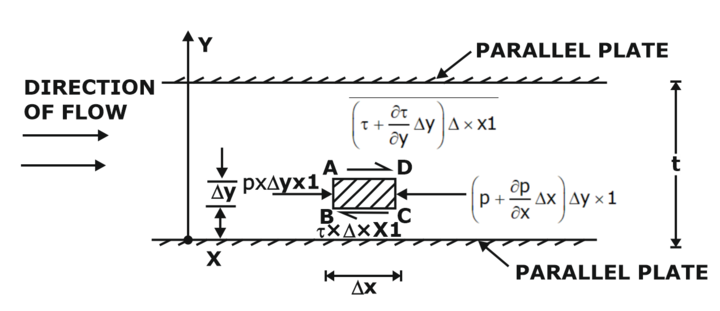
For steady and uniform flow, there is no acceleration; hence, the resultant force in the flow direction is zero.
∂τ/∂y = ∂P/∂x
Velocity Distribution (u)
the value of shear stress is given by
τ = μ du/dy and ∂τ/∂y = ∂P/∂x
Boundary condition, at y = 0 u = 0
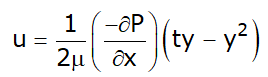
Thus, velocity varies parabolically as we move in the y-direction, as shown in Figure.
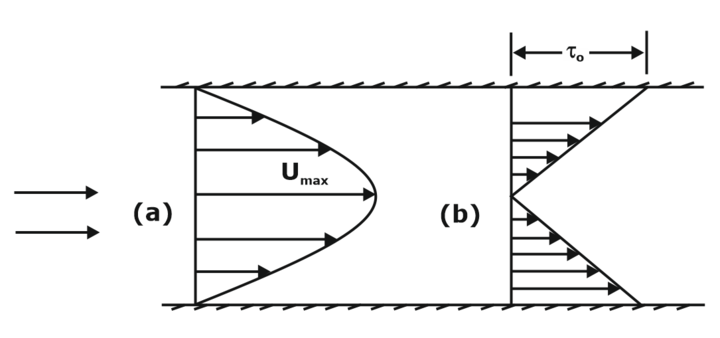
Velocity and shear stress profile for turbulent flow
At y = t/2; u = Umax
Umax = (1/8μ)(-∂P/∂x)t2
The ratio of Maximum velocity to average velocity:
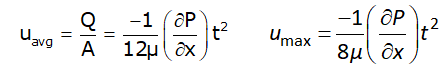
Thus,
Uavg = (2/3) Umax ⇒ Uavg/Umax = 2/3
The pressure difference between two parallel fixed plates
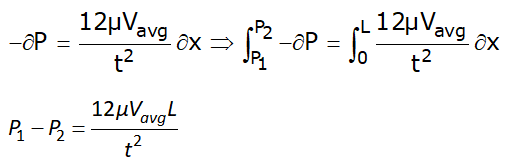
Different Correction Factors
Two correction factors include the momentum correction factor and the kinetic energy correction factor. These correction factors relate the flow’s actual behaviour with the flow’s behaviour based on the average velocity and are important for the GATE exam. These are described below:
- Momentum correction factor (β)
- Kinetic energy correction factor (α)
Momentum correction factor (β)
It is defined as the ratio of momentum per second based on actual velocity to the momentum per second based on average velocity across a section. It is denoted by β.

Kinetic energy correction factor (α)
It is defined as the ratio of the flow’s kinetic energy per second based on actual velocity to the flow’s kinetic energy per second based on average velocity across the same section.
Let p = momentum
P = momentum/sec.
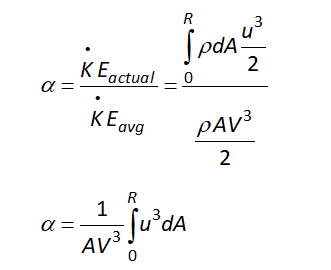
For flow through pipes values of α and β:
|
Correction-factor |
Laminar |
Turbulent |
|
α |
2 |
1.33 |
|
β |
1.33 |
1.2 |
From the above, we can say that the value of the correction factor for Laminar flow is more than that for turbulent flow.
Turbulent Flow Characteristics
Turbulent flow is a fluid flow categorized based on the Reynolds number of the flow. In turbulent flow, fluid particles are mixed with each other. Here a few turbulent flow characteristics are described.
In the case of turbulent flow, there are huge orders of intermission fluid particles; due to this, various fluid properties will change with space and time.
Difference Between Laminar and Turbulent Flow
Laminar and turbulent flow is the flow characteristics categorized based on the Reynolds number of the flow. In the laminar flow, fluid particles move in the layered form and in the turbulent flow, fluid particles are mixed with each other during its motion.
For the pipe flow, If the Reynolds number is less than 500, it will be considered as the laminar flow, and if the Reynolds number is greater than 2000, it will be considered as the turbulent flow, and for the in-between value of Reynolds number flow will be considered as the transition flow.
Average Velocity and Fluctuating Velocity in Turbulent Flow
Average velocity is the value for which the total discharge through a section remains the same as the actual discharge. And fluctuating velocity is the actual velocity in the turbulent flow. It is said to be fluctuating velocity because the direction and magnitude of the velocity vary in nature.
Boussinesq Hypothesis
Similar to the expression for viscous shear, J. Boussinesq expressed the turbulent shear mathematical form as
τt = η(duavg/dy)
where τt = shear stress due to turbulence
η = eddy viscosity
uavg = average velocity at a distance y from the boundary. The ratio of η (eddy viscosity) and (mass density) is known as kinematic eddy viscosity and is denoted by ϵ (epsilon). Mathematically it is written as
ε = η/ρ
If the shear stress due to viscous flow is also considered, then …. shear stress becomes as
τ = τv + τt = μ(du/dy) + η(duavg/dy)
The value of η = 0 for laminar flow.
Reynolds Expression for Turbulent Shear Stress
Reynolds developed an expression for turbulent shear stress between two layers of a fluid at a small distance apart, which is given as:
τ = ρu’v’
where u’, v’ = fluctuating velocity component in the direction of x and y, respectively, due to turbulence.
As u’ and v’ vary, τ will also vary.
Hence, the time average on both sides of the equation to find the shear stress.
τavg =(ρu’v’)avg
The turbulent shear stress given by the above equation is known as Reynold stress.
Prandtl Mixing Length Theory
According to Prandtl, the mixing length L is the distance between two layers in the transverse direction such that the lumps of fluid particles from one layer could reach the other layer and the particles are mixed in the other layer in such a way that the momentum of the particles in the direction of x is same.
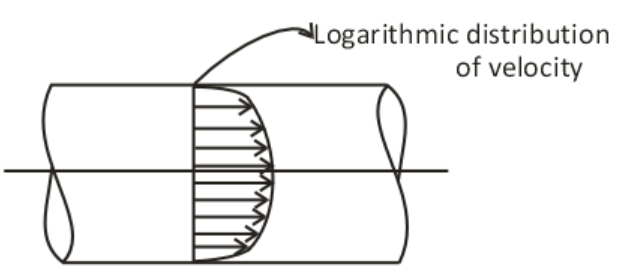
Velocity Distribution in Turbulent Flow
Velocity distribution in turbulent flow follows the logarithmic distribution. In the turbulent flow, the velocity at the boundary of the pipe is zero and maximum at the center of the pipe. It is shown in the below diagram.
(umax – u)/u* = 2.5 loge(R/y)
(umax – u)/u* = 2.5 × 2.303 log10(R/y)
(umax – u)/u* = 5.75 log10(R/y)
In the above equation, the difference between the maximum velocity umax, and local velocity u at any point, i.e. (umax – u), is known as a ‘velocity defect’.
Velocity distribution in turbulent flow through a pipe
Laminar sublayer thickness
Laminar sublayer thickness (δ’) = 11.6ν/u*
If you aim to crack GATE & ESE, Other PSU Exams, you must try Online Classroom Program to get unlimited access to all the live structured courses and unlimited mock tests from the following links.



