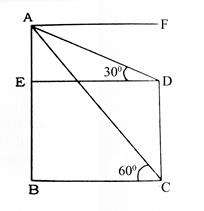
(1)Two poles of equal height are standing opposite to each other on either side of a road, which is 28m wide. From a point between them on the road, the angles of elevation of the tops are 300 and 600. The height of each pole is:
Ans. (d)
Let AB and CD be the pole and AC be the road.
Let AE = x, then EC = 28-x and AB = CD = h. Then let AB = CD=√3
then, EC =1 and AE = 3
AC (ratio value) = 3 + 1 = 4
4 = 28 then 1 =7
and √3=7√3 so height of tower is 7√3.
(2)There are two vertical posts, one on each side of a road, just opposite to each other. One post is 108 metre high. From the top of this post, the angles of depression of the top and foot of the other post are 300 and 600 respectively. The height of the other post is :
(a)36
(b)72
(c)76
(d)80
Ans (b)
The height of greater Lower i.e. AB = 108 = H
so height of tower is 72
(3)An aeroplane when flying at height of 5000 m from the ground passes vertically above another aeroplane at an instant, when the angles of elevation of the two aeroplanes from the same point on the ground are 600 and 450 respectively. The vertical distance between the aeroplanes at that instant is:
(d)4500 m
Ans (c)
In this question we have two triangle ABC and triangle DBC. In triangle ABC we apply the ratio according to 60° and in triangle DBC we apply ratio according to the 45°. That why we take AB=√3 and DB =1.
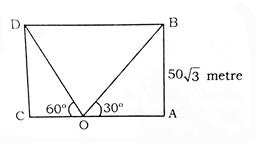
(4)A boy standing in the middle of a field, observes a flying bird in the north at an angle of elevation of 300 and after 2 minutes, he observes the same bird in the south at an angle of elevation of 600. If the bird flies all along in a straight line at a height of then its speed in km/h is:
(a) 4.5
(b) 3
(c) 9
(d) 6
Ans.(d)
In ABO
According to ratio method
From triangle DCO
DO cot AO = 150 + 50 = 200 m
(5)A tree is broken by the wind. If the top of the tree struck the round at an angle of 300 and at a distance of 30 m from the root, then the height of the tree is :
Ans. (b)
√3=30
1= 10√3 & 2 =20√3
so total height is 1+2 =10√3+20√3= 30√3
(6)The angle of elevation of a cloud from height h above the level of water in a lake is a and the angle of the depression of its image in the lake is b. Then, the height of the cloud above the surface of the lake is :
Ans. (d)
Let P be the cloud at height H above the level of the water in the lake Q its image in the water
B is at a point at a height AB = h, above the water, Angle of elevation of P and depression of Q from B are respectively
In triangle PBM
From equations (i) and (ii),





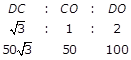








Comments
write a comment