Memory Based CSIR NET Mathematics Question Paper 2023, 7th June Download PDF
By BYJU'S Exam Prep
Updated on: September 13th, 2023

CSIR NET Mathematics Memory Based Questions 2023: The CSIR NET Mathematics Exam 2023 was conducted on the second day of the exam on 7th June in shift 2. Here is the list of CSIR NET Mathematics Memory Based Questions that were asked in the examination today.
We have also developed a detailed article on the CSIR NET Mathematics Exam Analysis for parts A, B, and C. The candidates can check the article for the CSIR NET Mathematics Question paper 2023 below and download the PDF for future reference.
Table of content
Key Highlights of CSIR NET Mathematics Memory Based Questions
- The CSIR NET 2023 Mathematics Exam was conducted in shift 2 from 3:00 PM to 6:00 PM on 7th June 2023.
- The CSIR NET Mathematics Paper contained 120 questions. The candidates had to attempt 60 questions in total.
CSIR NET Mathematics Memory Based Questions: Part A
The candidates can check a detailed analysis of the questions asked in the CSIR NET Mathematics for Part A with all the details on the topics. The table below contains the questions from Part A of the CSIR NET Mathematics Exam.
| Questions | Topic |
| Which of the option correctly represents the relationship between: Insects, peacock, birds, extinct animals? | Venn Diagram |
| Find the total interest on Rs. 150,000 for 3 years at a rate of interest is 10% p.a. | Interest |
| A candidate has a 30% chance of saying the truth. B candidate has a 40% chance of saying the truth. What is the probability that both A and B candidates contradict? | Probability |
CSIR NET Mathematics Memory Based Questions: Part B and C
The candidates can check a detailed analysis of the questions asked in the CSIR NET Mathematics for Part B & C with all the details on the topics.
| Questions Asked | Topics |
|
How many real roots are there in polynomial |
polynomial Ring |
|
Matrix 3X3 is a real entity then, which of the following is not true.
|
Matrices & Its properties |
| Linear transformation on polynomial defined as derivative then which is true? | Linear Transformation |
|
Quadratic form
|
Quadratic Form |
 |
Complex Integration |
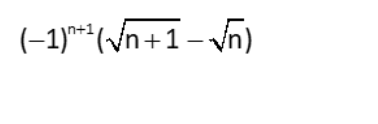 |
Sequence & Series |
 |
Wave Equation |
|
Possible Class equation for group of order 10
|
Class Equation |
|
an = 1/n+1+1/n+2…..+1/2n bn = 1/n Are seq then
|
Sequence & Series |
 |
Sequence & Series |
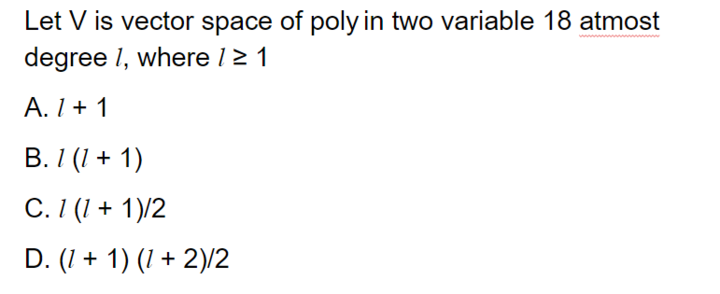 |
Vector Space |
|
uvx + vy = 0 u(x, 0) = x u(2, 3) = ? |
Cauchy Problem |
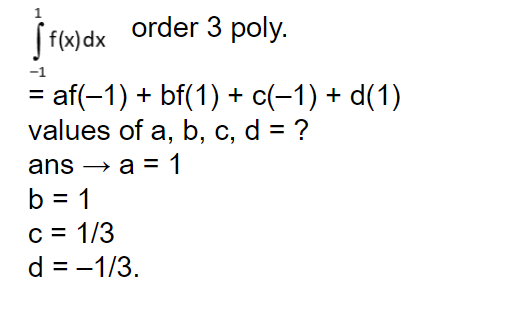 |
Numerical Integration |
|
Which of the following statements is/are true ??
|
Topology |
|
_One measure theory Question_ If A is a non-empty subset of [0,1] then which of the following is/are true?
|
Measure Theory |
|
A is matrix of 3 × 3 order and P(T) is ch poly of A which is divisible by T² then is a matrix of 3 × 3 order and P(T) is ch poly of A which is divisible by T² then
|
Eigen Value & Matrices |
CSIR NET Mathematics Memory Based Questions: Download PDF
The candidates can click on the link provided below to download the PDF for today’s CSIR NET Memory-Based Questions asked in the exam. This will give them a better sense of the difficulty level of the exam and even help future candidates prepare.
> CSIR NET Mathematics Memory Based Question Paper – Download PDF


