Matrix Method
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Matrix Method is one of the two methods for analysing the indeterminate structure, depending on the unknown chosen for analysis. If the unknown is taken as forces, it is known as the force method (Flexibility method), and if the unknown is taken as displacements, it is known as the displacement method (Stiffness method). The matrix method of analysis of indeterminate structures provides a tool for solving the differential equations used in the analysis. In the matrix method, unknowns are written in terms of the matrix element, and it can be solved using the concept of matrix algebra.
Based on the type of unknowns used in the matrix, it can be classified as the flexibility and stiffness matrix methods. These methods of analysis of indeterminate structures will be discussed in this article. Matrix methods for analysing indeterminate structures are based on the principle of matrix algebra, And they can also be implemented in terms of computer programing. Due to its advantages, many software applications use the matrix method to analyse indeterminate structures.
Table of content
What is Matrix Method?
The Matrix method of structural analysis is a method used for the analysis of indeterminate structures. A matrix is a tool for solving many civil engineering analysis problems. And elements of the matrix are based on either flexibility or stiffness coefficients. Based on the coefficient used as the matrix element, it can be classified as the flexibility and stiffness matrix methods. The matrix method is essential for the GATE question paper. These coefficients are based on the compatibility conditions of the structure.
These methods analyse large structures, like multi-story buildings, railway bridges, and other large structures where analysis becomes complex. With the help of these methods, redundant forces can be determined in a structure, and with the help of that, forces and displacement analysis can be done.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Solution of an Equation by Matrix Method
Matrix methods are based on matrix algebra, and the matrix elements are flexibility and stiffness coefficients. These coefficients are based on the compatibility conditions of the indeterminate structure. Using various matrix operations, these unknown elements (redundant forces or displacements) can be found easily, and structural analysis can be done with the help of that. Matrix operation consists of addition, subtraction, etc. A system of linear equations in the matrix method of analysis can be solved with the help of these matrix operations.

Download Formulas for GATE Civil Engineering – Fluid Mechanics
What are the Different Types of Matrix Methods?
In the case of the matrix method, unknown parameters of structures are solved with the help of matrix concepts. Based on the parameters of the matrix element, it is classified as the flexibility matrix method and displacement matrix method. Various matrix methods are mentioned in the GATE CE syllabus. These methods are described below:
Flexibility Matrix Method
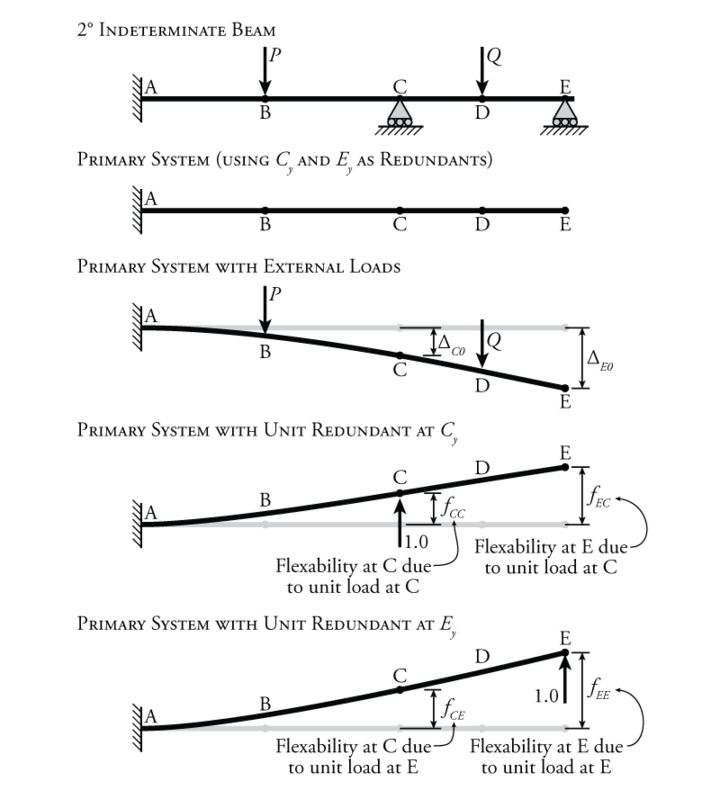
The flexibility matrix method is also a method of analysis of indeterminate structures. This method comes under the force method of analysis. In this method, forces are taken as unknown, and equations are expressed in terms of these forces. An additional compatibility condition equation is developed to find all the unknown forces. This method is suitable when the static indeterminacy is less than kinematic indeterminacy.
Flexibility (δ)
Flexibility is defined as the displacement produced due to unit force. It is the inverse of stiffness. Flexibility for various cases is as follows
(1) Axial flexibility= L/AE
(2) Transverse flexibility= L3/12AE
(3) Flexural flexibility= L/4AE
(4) Torsional flexibility= L/GJ
Displacement or Stiffness Matrix Method
The stiffness matrix method comes under the displacement method of analysis of indeterminate structures. In this method, displacements at the joints are taken as unknowns, and equations are expressed in terms of these unknown displacements. Additional joint equilibrium equations are developed to find the unknown displacement. This method is suitable when the Kinematic indeterminacy is less than the static indeterminacy.
Stiffness (k)
It is the load required to produce unit displacement. The stiffness for various cases is as follows.
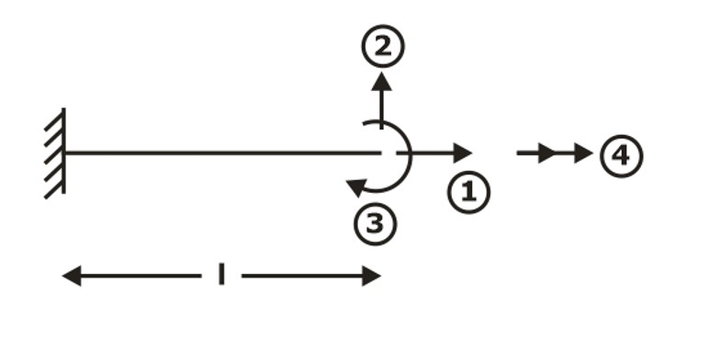
(1) Axial stiffness (k11) = AE/L
(2) Transverse stiffness (k22) = 12EI/L3
(3) Flexural stiffness (k33) = 4EI/L
(4) Torsional stiffness (k44) = GJ/L
Advantages of Matrix Methods of Analysis
As we know, the concept of matrix algebra can be used in the matrix method of analysis of indeterminate structures. Hence it provides a well-defined approach to solving the unknowns of equations used in the GATE exam. In the case of indeterminate structures, compatibility equations are also used along with the equilibrium equations for the analysis. Some advantages of this method are listed below:
- These methods are based on the matrix, giving a simpler procedure for analysing indeterminate structures.
- Computer programming for this method can be written, so these methods can solve complex equations.
Matrix Method Example
As we have discussed, the matrix method for analysing indeterminate structures can be used for solving complex equations. So, it is very important to understand this method. Analysis of indeterminate structures by matrix method is based on finding out the flexibility or stiffness coefficients. Here an example is shown that illustrates the concept of these coefficients.