Radiation Heat Transfer

What is Radiation Heat Transfer?

The process of transferring heat through Electromagnetic Radiation, which is generated by the thermal motion of particles in matter, is known as thermal Radiation. This particular electromagnetic Radiation is found in the infrared area of the spectrum, which is invisible to most bodies on Earth. Thermal Radiation is emitted by every particle having a temperature greater than absolute zero, and the mobility of particles inside the body is what causes thermal Radiation. This motion is wholly stopped at absolute zero, which is why a body at absolute zero does not admit any radiation, whereas anything above absolute zero does.

Radiation Heat Transfer Definition

Radiation heat transfer is when energetic particles or waves travel through a medium or space and transmit heat. Because the transmission mechanism is photon emission, unlike conduction and convection, there needs to be no intermediate matter to enable transmission.

Radiation heat loss is the difference between the energy state before and the energy that is radiated after. Thermal Radiation is mainly responsible for the glowing quality of hot objects, with iron being referred to as "red hot" because most of the body's thermal energy at that temperature falls in the red band of the spectrum. It will begin to emit a distinct colour at even higher temperatures. It's an exciting story about how heat radiation was discovered. William Herschel, an English astronomer, discovered it when he moved a thermometer from one aperture of a prism spectrum to another.

Download Formulas for GATE Mechanical Engineering - Thermodynamics

Properties of Radiation Heat Transfer

Radiation is the energy emitted by matter in the form of electromagnetic waves resulting from changes in the electronic configurations of atoms and molecules. Four key characteristics define thermal Radiation or Radiation heat transfer.

• At any temperature, a body's thermal Radiation emits various frequencies. Planck'sPlanck-body radiation equation gives an idealised emitter's frequency distribution.
• As the temperature of the emitter rises, the primary frequency (or colour) range of the emitted Radiation moves to higher frequencies. A red hot item, for example, radiates primarily in the visible band's wavelengths (red and orange). It begins to produce detectable amounts of green and blue light as it heats up further, and the dispersion of frequencies over the visible range causes it to seem white to the human eye; it is white-hot. Even at a white-hot temperature of 2000 K, 99 per cent of the Radiation'sRadirgy is still infrared. Wien'sWien'splacement law determines this.
• As the temperature rises, the total amount of Radiation of all frequencies increases sharply; it rises as T⁴, where T is the body's absolute temperature.
• Reciprocity describes how the rate of electromagnetic Radiation released at a particular frequency is related to the quantity of absorption experienced by the source. As a result, a surface that absorbs more red light emits more red light when heated.

Stefan-Boltzmann Law

The entire amount of Radiation (all wavelength range radiations) emitted by a body per unit area and time is known as the emissive power. According to Stefan- Boltzmann, the emissive power of a black body is proportional to absolute temperature to the fourth power.

Download Formulas for GATE Mechanical Engineering - Fluid Mechanics and Machinery

Blackbody Radiation

• A blackbody is defined as a perfect emitter and absorber of Radiation. No surface can emit more energy at a specified temperature and wavelength than a black body.
• A blackbody is a diffuse emitter which means it emits Radiation uniformly in all directions and absorbs all incident Radiation regardless of wavelength and direction.
• The radiation energy emitted by a blackbody per unit of time and per unit of surface area can be determined by the Stefan-Boltzmann Law

E_b = σAT⁴

Where

• σ = Radiation Heat Transfer Coefficient or Stefan Boltzmann constant, σ = 5.67 × 10-8 W/m² K⁴
• T is the absolute temperature of the surface in K
• E_b is called the blackbody emissive power.

Black Body Thermal Radiator's Subjective Color

William Herschel discovered that the temperature had changed. The most significant temperature recorded fell below the visible light spectrum's band. As a result, the term "infrared waves" was coined. Infrared waves, on the other hand, should not be mistaken for heat waves. The subjective colours about temperature are as follows:

Kirchhoff's Law

• Consider an isothermal cavity and a surface at the same temperature, T. At the steady state (equilibrium) thermal condition

G_abs = αG = ασT⁴

and Radiation emitted

E_emit = εσT⁴

Since the small body is in thermal equilibrium

G_abs = E_emit

ε(T) = α(T)

• The total hemispherical emissivity of a surface at temperature T equals its total hemispherical absorptivity for Radiation coming from a blackbody at the same temperature T. This is called Kirchhoff's Law.

• Kirchhoff's law makes the radiation analysis easier (ε = α), especially for opaque surfaces where ρ = 1 – α. Kirchhoff's law cannot be used when there is a significant temperature difference (more than 100 K) between the surface and the source temperature.
• Kirchhoff's law cannot be used when there is a significant temperature difference (more than 100 K) between the surface and the source temperature.

Solar Radiation

• The solar energy reaching the edge of the Earth'sEarth'sosphere is called the solar constant:

G_s = 1353 W / m²

• The effective surface temperature of the sun can be estimated from the solar constant (by treating the sun as a black body).
• The solar Radiation undergoes considerable attenuation as it passes through the atmosphere as a result of absorption and scattering:
  • Absorption by the oxygen occurs in a narrow band about λ = 0.76 µm.
  • The ozone layer absorbs ultraviolet Radiation at wavelengths below λ = 0.3 µm almost entirely and Radiation in the range of 0.3 – 0.4 µm considerably.
  • Absorption in the infrared region is dominated by water vapour and carbon dioxide. Dust/pollutant particles also absorb Radiation at various wavelengths.
  • As a result, the solar radiation reaching the Earth'sEart'sface is about 950 W/m2 on a clear day and much less on a cloudy day, in the wavelength band 0.3 to 2.5 µm.
• The gas molecules (mainly CO2 and H2O) and the suspended particles in the atmosphere emit Radiation and absorb it. Considering the atmosphere (sky) as a black body at some lower temperature is convenient. This fictitious temperature is called the effective sky temperature T_sky.

G_sky = σ T⁴_sky

• T_sky = 230 K for a cold clear sky
• Tsky = 285 K for warm, cloudy sky

Using Kirchhoff'sKir'w, we can write α = ε since the sky's temperature is on the order of the room temperature.

Rules in Radiation Heat Transfer

• F_i→j or Fij = the fraction of the Radiation leaving surface i that strikes surface j directly.

• F_ij = 0 indicates that two surfaces do not see each other directly.
• F_ij = 1 indicates that surface j surrounds surface i.
• The Radiation that strikes a surface does not need to be absorbed by that surface.
• F_ii is the fraction of Radiation leaving surface i that strikes itself directly.
• F_ii = 0 for plane or convex surfaces, and Fii ≠ 0 for concave surfaces.

Fig. above shows the View factor between the surface and itself.

View Factor Relations

• Radiation analysis of an enclosure consisting of N surfaces requires the calculations of N² view factors.
• Once a sufficient number of view factors are available, the rest can be found using the following relations for view factors.

The Reciprocity Rule

• The view factor F_ij is not equal to F_ij unless the areas of the two surfaces are equal. It can be shown that: A_i F_ij =A_j F_ij

The Summation Rule

• In radiation analysis, we usually form an enclosure. The conservation of energy principle requires that the entire Radiation leaving any surface i of an enclosure be intercepted by the surfaces of the enclosure. Therefore,

^N∑_j=1 F_ij = 1

• The summation rule can be applied to each surface of an enclosure by varying i from 1 to N (number of surfaces). Thus the summation rule gives N equations. Also reciprocity rule gives 0.5 N (N-1) additional equations. Therefore, the total number of view factors that need to be evaluated directly for an N-surface enclosure becomes: N² - [N + 1/2[N(N-1)]] = 1/2[N(N-1)]

The Superposition Rule

• The view factor from a surface i to a surface j equals the sum of the view factors from surface i to the parts of surface j.

Fig above shows the superposition rule for view factors.

F_1→(2,3) = F_1→2 + F_1→3

The Symmetry Rule

• Two (or more) surfaces that possess symmetry about a third surface will have identical view factors from that surface.

For eg. the view factor from the base of a pyramid to each of its four sides. The base is a square, and its side surfaces are isosceles triangles

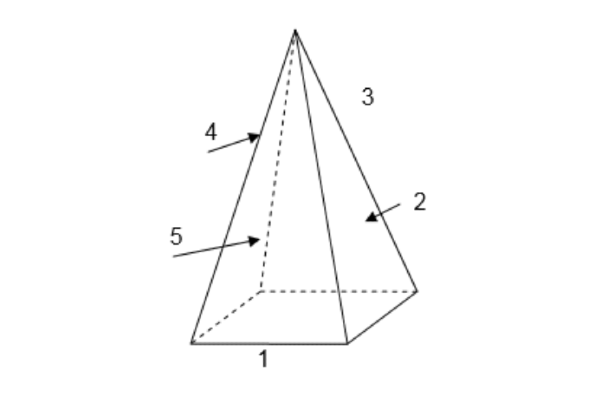
From the symmetry rule, we have:

F₁₁ = F₁₂ = F₁₃ = F₁₄ = F₁₅

• Also, the summation rule yields: F₁₁ + F₁₂ + F₁₃ + F₁₄ + F₁₅ = 1
• Since, F₁₁ = 0 (flat surface), we find
• F₁₂ = F₁₃ = F₁₄ = F₁₅ = 0.25

The Crossed-Strings Method

Geometries such as channels and ducts that are very long in one direction can be considered two-dimensional (since Radiation through end surfaces can be neglected). The view factor between their surfaces can be determined by the crossing method developed by H. C. Hottel, as follows:

F_i→j = [∑( Crossed String) - ∑( Uncrossed String)] /[2* (Strings o surface i)]