What are Universal Gates? NAND and NOR Gate
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Universal Gates may implement any Boolean function without using any other gate type. The NAND gate and NOR gate are called Universal gates because they can perform all the three essential functions of AND, OR and NOT gates.
A two-input NAND gate is a digital combination logic circuit that performs the logical inverse of an AND gate. While an AND gate outputs a logical “1” only if both inputs are logical “1,” a NAND gate outputs a logical “0” for this same combination of inputs. Here, we will explore the Universal gates, NAND Gate & NOR Gate, along with a few examples of each.
Download Formulas for GATE Computer Science Engineering – Programming & Data Structures
Table of content
What are Universal Gates?
Universal gates are those gates that can perform the tasks of other gates with minor adjustments. Universal gates are widely used in formulating NAT-based questions in the GATE exam. There are two universal gates:
- NAND Gate
- NOR Gate
Let us understand these universal gates in detail in the coming sections.
Download Formulas for GATE Computer Science Engineering – Discrete Mathematics
NAND Gate
The NAND gate is one of the universal gates. The NAND gate is a AND gate followed by a NOT gate. Thus, we can say it is a AND NOT operation. It may have two or more inputs but only one output. The logical symbols of a NAND Gate and the truth table are shown below.

- Thus, the logical expression for the output is
![]()
It is clear from the truth table of the two-input NAND gate that the output is 1 when either A or B or both the inputs are at logic ‘0’. We can say that if Ā = 1 = B are, both A and B are 1, and the output is 1. Therefore, the NAND gate can perform the OR function by inverting the inputs.
- The output is the exact inverse of the AND gate for all possible input combinations in the NAND gate.
- The OR gate with inverted inputs is called bubbled OR gate or negative OR gate. The NAND gate is also called an active low OR gate.
- The switching circuit diagram for a NAND gate is shown below:
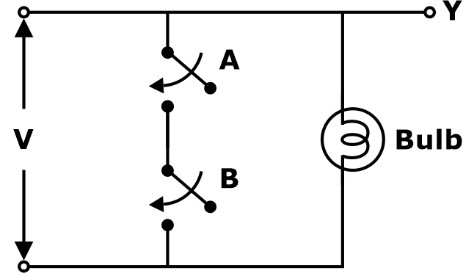
The bulb will glow when any of the switches A or B will open (logic 0).
- NAND gate follows the commutative law as (AB)’ = (BA).’
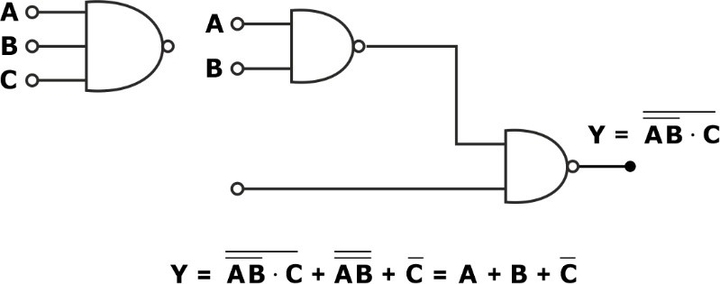
- NAND gate will not follow the associative law as
- Enable and disable inputs:
For a NAND Gate

For control = 0;
|
A |
Control |
Y |
|
0 |
0 |
1 |
|
1 |
0 |
1 |
Thus, logic ‘0’ is the disabled input for the NAND gate.
For control = 1;
|
A |
Control |
Y |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
Thus, logic ‘1’ is the enable input for the NAND gate.
Download Formulas for GATE Computer Science Engineering – Algorithms
NOR Gate
The NOR gate is one of the universal gates. A NOR gate combines two basic logic gates: an OR gate and a NOT gate. So we can say it is an OR-NOT operation. It may have two or more inputs and an output. The logical symbols of the NOR Gate are shown:

- It is clear from the truth table that the output is ‘1’ only if all the inputs are at logic ‘0’. It can also say that if the inputs A’ = B’ = 1, the output Y is 1. Thus, the NOR gate is equivalent to the AND gate with inverted inputs, and it can be realized by a bubbled AND gate, as shown above.
- The logical expression for the output is
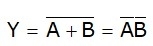
- The NOR gate is also called as the active LOW AND gate.
- The switching circuit of a NOR gate is as shown:
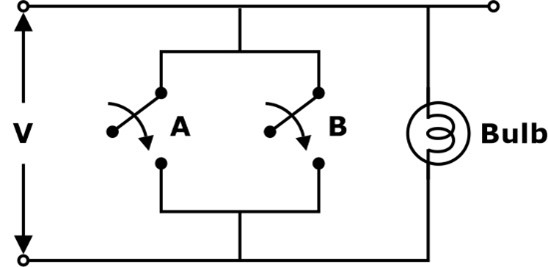
When any of the switches, either A or B, is closed, the bulb will not glow.
- NOR gate follows the commutative law as follows:
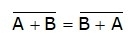
However, it does not follow the associative law.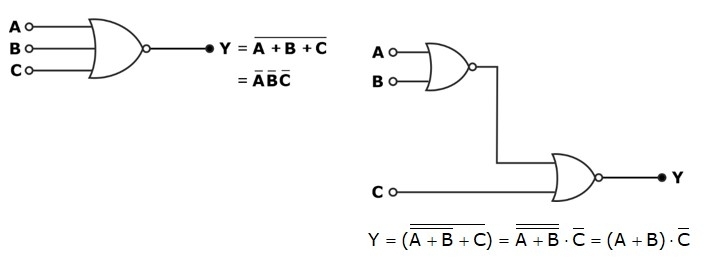
- Enable and disable inputs:
For a NOR Gate

If control = 0;
|
A |
Control |
Y |
|
0 |
0 |
1 |
|
1 |
0 |
0 |
Thus, logic ‘0’ enables input.
If control = 1;
|
A |
Control |
Y |
|
0 |
1 |
0 |
|
1 |
1 |
0 |
Thus, logic ‘1’ is disabled input.
Realization of the Logic Gate Using NAND Gate and NOR Gate
The realization of the logic gates is essential to the GATE CSE syllabus. These realizations using the NAND gate and NOR gate will help in building the strong conceptual base for the forthcoming exam.
NOT Gate Realization
Using NAND Gate
For the NOT gate realization, we require 1 NAND gate, as shown in the circuit diagram:
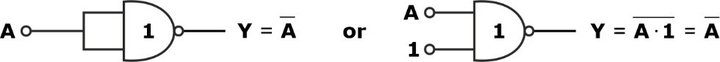
Using NOR Gate
For the NOT gate realization, we require 1 NOR gate, as shown in the circuit diagram:

AND Gate Realization
Using NAND gate
For the AND gate realization, we require 2 NAND gates, as shown in the circuit diagram:

Using NOR Gate
For the AND gate realization, we require 3 NOR gates if the inputs are not available in complement form, as shown in the circuit diagram:
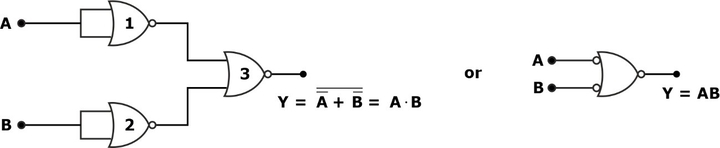
OR Gate Realization
Using NAND Gate
For the OR gate realization, we require 3 NAND gates if the inputs are not available in complement form, as shown in the circuit diagram:
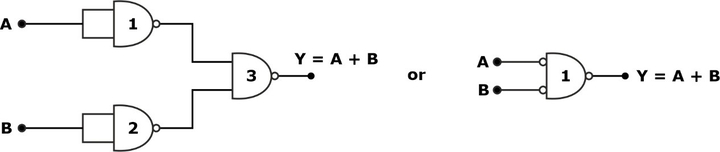
Using NOR Gate
For the OR gate realization, we require 2 NOR gates, as shown in the circuit diagram:

EX-OR Gate Realization
Using NAND Gate
For the EX-OR gate realization, we require 4 NAND gates, as shown in the circuit diagram:
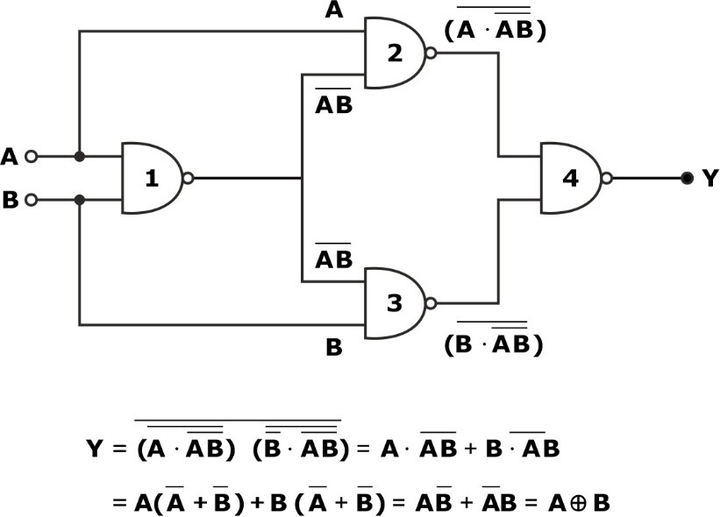
Using NOR Gate
For the EX-OR gate realization, we require 5 NOR gates, as shown in the circuit diagram:
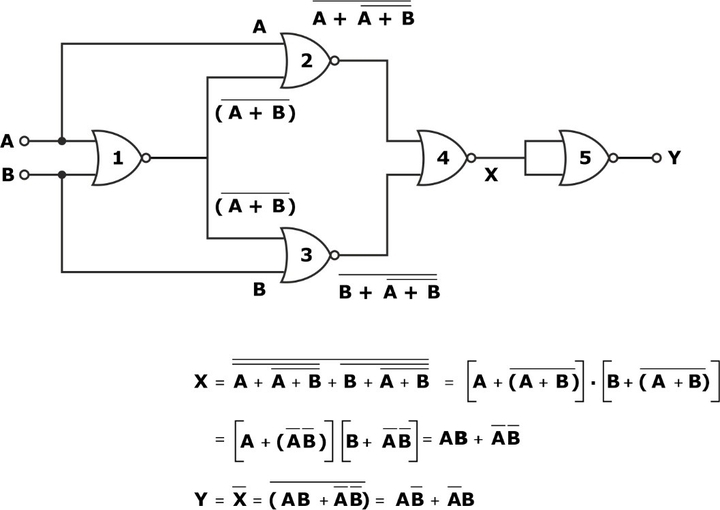
EX-NOR Gate Realization
Using NAND Gate
For the EX-NOR gate realization, we require 5 NAND gates, as shown in the circuit diagram: 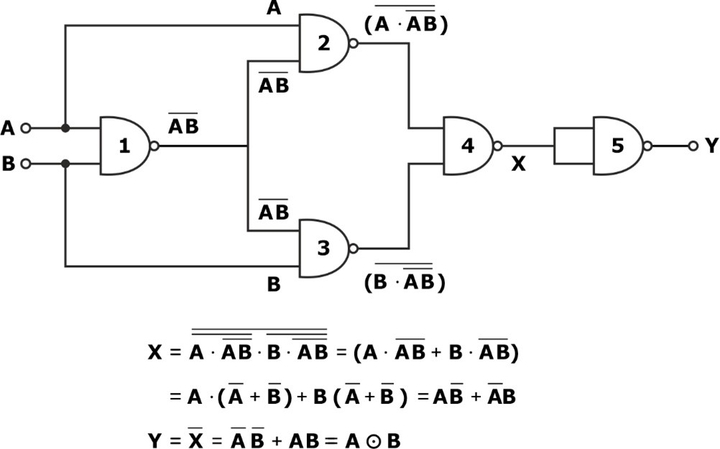
Using NOR Gate
For the EX-NOR gate realization, we require 4 NOR gates, as shown in the circuit diagram:
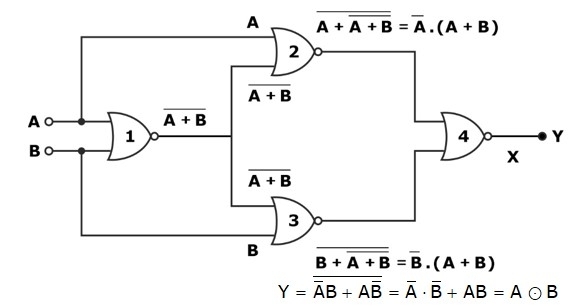
NOR Gate Realization Using NAND Gate
For the NOR gate realization using the NAND gate, we require 4 NAND gates, as shown in the circuit diagram:
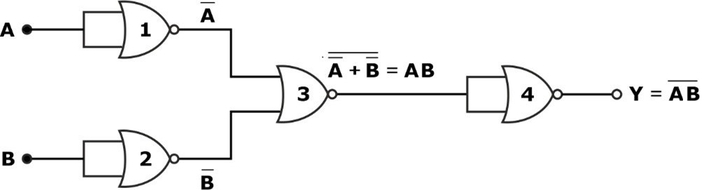
NAND Gate Realization Using NOR Gate
For the NAND gate realization using the NOR gate, we require 4 NAND gates, as shown in the circuit diagram:
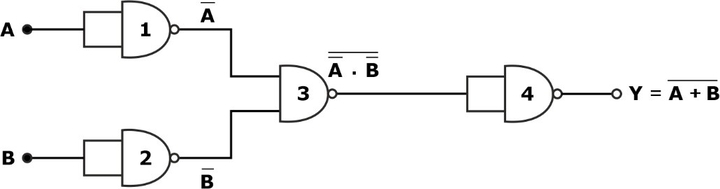
Shortcuts for the realization of logic gates are as follows:
|
GATES |
Number of NAND gate |
Number of NOR gate |
|
NOT |
1 |
1 |
|
AND |
2 |
3 |
|
OR |
3 |
2 |
|
EX-OR |
4 |
5 |
|
EX-NOR |
5 |
4 |


