Question. A certain sum of money at simple interest works out to Ps. 1012 in 2.5 years and to Rs. 1067.20 in 4 years. Then find the rate of interest?
Question. A certain amount of money at r% compounded annually after two and three years becomes Rs. 1440 and Rs. 1728 respectively. Then find the value of r.
Solution:
I the principal be Rs. P, then
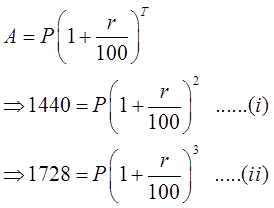
On dividing equation (ii) by (i),
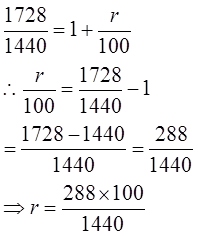
= 20% per annum
Short Trick:
Subtract the amount of 2yrs from the amount of 3 yrs
1728 - 1440 = 288
= 288x100/1440 = 20%
Question. If a man receives simple interest on one-fourth of his capital 3% interest, on two third 5% and on the remainder 11%, then find the percentage he receives on the whole in a year for the complete amount?
Question. A bank gives compound interest on deposits at the rate of 5% for the first year, 6% for the second year and 10% for the third year. If a deposit amounts to ₹12,243 at the end of the third year, then what was the initial deposit?
Question.Find the time in which 80,000 amounts to 92,610 at 10% p.a. at compound interest, interest being compounded semiannually?
Question. At a certain rate of simple interest, a certain sum of money becomes double of itself in 10 years. After how many years it will treble itself ?










Comments
write a comment