In this part, we will try to solve questions with the help of ratio. This trick will save a lot of time and useful during the exam period. This article also contains some useful formula.
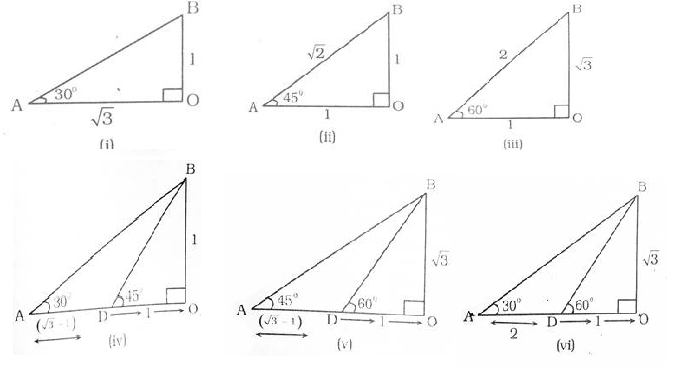
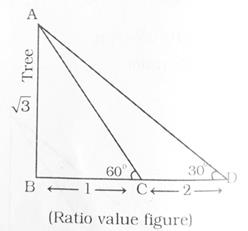
Here are some ratio figure which you have to remember
Important short tricks are :
Note: ![]() only when the sum of angle i.e
only when the sum of angle i.e ![]()

Some Important questions are as follows:
Example 1:The angle of elevation of the top of a tower at a distance of 500 m from its foot is 30°. The height of the tower is :
(c)500
Ans. (d)
Short trick:
Solve it with ratio, as the angle of elevation is 30° then ratio between P: B: H is 1:√3:2 so √3= 500 then 1= 500/√3 and height is equal to ![]()
Example 2: The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 450 and reaches the opposite bank at a point 20 m from the point opposite to the starting point. The breadth of the river is :
(a) 20 m
(b) 28.28 m
(c) 14.14 m
(d) 40 m
Ans. (c) 14.14 m
Solution:
Let A be the starting point and B, the endpoint of the swimmer. Then AB = 20m & ![]()
Short Method;
AS the angle of elevation is 45° then the ratio of P: B : H i.e. 1:1:√2
here √2 =20 then 1 =20/√2
Question 3: A man from the top a 50m high tower, sees a car moving towards the tower at an angle of depression of 300. After some time, the angle of depression becomes 600. The distance (in m) travelled by car during this time is –
Ans. (c)
Solution:
AB = AC – BC
Example 4:A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite side of the bank is 600. When he moves 50m away from the bank, the angle of elevation becomes 300. The height of the tree and width of the river respectively are :
(c) ![]()
(d) None of these
Answer: c)
Solution:
Ratio value original value
height of the tree= h (ratio value = ![]() )=
)=![]()
and width of the river = x (ratio value = 1) = 25 m
Example 5: From the top of a pillar of height 80 m the angle of elevation and depression of the top and bottom of another pillar are 300 and 450 respectively. The height of the second pillar (in metre) is:
Answer: (c)
Solution:
Let AB and CD are pillars.
Let DE = h
Required height





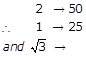

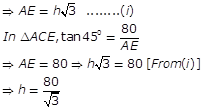




Comments
write a comment