- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Manometry and Buoyancy Study Notes for Mechanical Engineering
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Manometry and buoyancy is the term related to fluid statics. The concept of manometry and buoyancy is important to know the stability of a floating body and also for understanding the submerged conditions of a floating body. Archimedes’ principle is used to understand the concept of manometry and buoyancy.
Manometry and Buoyancy are two different terms that refer to the floating behavior of an object in a fluid. The concept of Manometry is used in the pressure measurement in fluid static, but the concept of buoyancy is related to the floating of a body in a static fluid. This article contains basic notes on the “Manometry and Buoyancy” topic of the “Fluid Mechanics & Hydraulics” subject.
Table of content
What are Manometry and Buoyancy?
Manometry and buoyancy are used for two different topics of fluid statics. Manometry refers to the pressure measurement of the fluid when it is in static condition. And buoyancy is a term related to the floating body.
Principle of Manometry
Manometers use the relationship between pressure and the head to measure the pressure of a static fluid. The principle of Manometry is essential for the GATE exam. It is based on the following principle.
- The pressure is proportional to the height of a column of fluid.
- Manometry is the field of science that deals with the evaluation of the pressure of the fluid.
- The instrument used to carry out the complete process is termed a Manometer.
- Types of Manometers: Barometer, Piezometer and U-tube Manometer.
Relation Between Hydrostatic Pressure and Head
Hydrostatic pressure is the pressure of the fluid when it is in a static condition. The pressure of the fluid is measured in terms of the height of the fluid column. The most common fluid for the head measurement is mercury and water. Mercury can represent very high pressure with the short length of the mercury column.
We have the vertical pressure relationship p = ρgz + constant measuring z from the free surface so that z = -h and surface pressure is atmospheric, patm
Pressure at the z depth below the free surface of the fluid (P) = ρgh + patm
We generally assume atmospheric pressure as the datum
Gauge pressure, pg = ρgh
The lower limit of any pressure is the pressure in a perfect vacuum. Pressure measured above a perfect vacuum (zero) is known as absolute pressure.
Absolute pressure, pa = ρgh+ patmospheric
Absolute pressure = Gauge pressure + Atmospheric
Types of Manometers
Manometers are classified based on the geometry of the manometers and the principle of the pressure measurements. Based on these parameters, manometers are classified into the following types.
Piezometer Tube Manometer
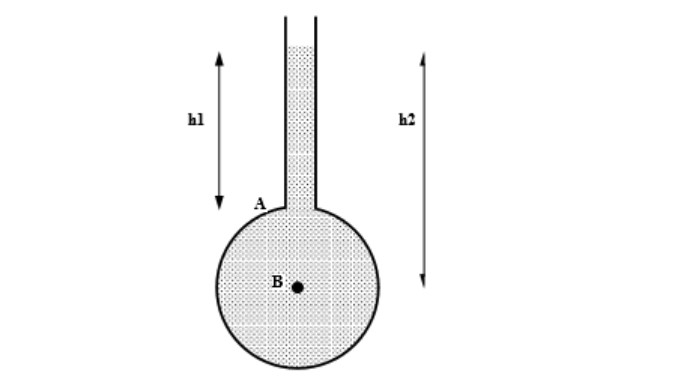
- The simplest manometer is an open tube. This is attached to the top of a container with liquid at pressure. containing liquid at a pressure.
- The tube is open to the atmosphere; the pressure measured is relative to the atmosphere, so it measures gauge pressure.
- Pressure at A = pressure due to column of liquid h1
pa = ρgh1
- Pressure at B = pressure due to column of liquid h2
Pb = ρgh2
Limitations of Piezometer
- It can only be used for liquids
- Pressure must be above atmospheric
- Liquid height must be convenient, i.e., not be too small or too large
U-tube Manometer

- It consists of a U-shaped bend whose one end is attached to the gauge point ‘A’ and the other is open to the atmosphere.
- It can measure both positive and negative (suction) pressures.
- “U”-Tube enables the pressure of both liquids and gases to be measured. “U” is connected as shown and filled with manometric fluid.
Note:
- The manometric fluid density should be greater than that of the fluid measured, ρman > ρ
- The two fluids should not be able to mix. They must be immiscible.
- Pressure in a continuous static fluid is the same at any horizontal level, pressure at B = pressure at C
PB = PC
- For the left-hand arm pressure at B
- pressure at A + pressure of height of liquid being measured
PB = PA + ρgh1
- For the right-hand arm pressure at C =
- pressure at D + pressure of height of manometric liquid
PC = P + ρmanogh2
We are measuring gauge pressure. We can subtract patmospheric giving
PB = PC
PA = P +ρmanogh2– ρgh1
Differential U-Tube Manometer
- A U-Tube manometric liquid is heavier than the liquid for which the pressure difference is to be measured and is not immiscible with it.

- The equation gives the pressure difference between A and B
PA – PB = ρ2h2 + ρ3h3 – ρ1h1
Inverted U-Tube Manometer
- An inverted U-Tube manometer consists of an inverted U-Tube containing a light liquid.
- This is used to measure the differences in low pressures between two points where better accuracy is required.
- It generally consists of an air cock at the top of the manometric fluid type.

The pressure difference can be calculated from the equation:
P1 – ρ1gH2 – ρmg(H1– H2)=P2 – ρ2gH1
Micro Manometer
- Micro Manometer is the modified form of a simple manometer whose one limb is made of a larger cross-sectional area.
- It measures very small pressure differences with high precision.

Let ‘a’ = area of the tube, A = area of the reservoir, h3 = Falling liquid level reservoir,
h2 = Rise of the liquid in the tube,
- By Volume Equality, Ah3 = ah2
- Equating pressure heads at datum,
P1 = (ρm – ρ1)gh3 + ρmgh2 – ρ1gh1
Inclined Manometer
- An inclined manometer is used for the measurement of small pressures and is to measure more accurately than the vertical tube-type manometer.
- Due to inclination, the distance moved by the fluid in the manometer is more.

- The equation gives the pressure difference between A and B
PA – PB = ρ2LsinΘ + ρ3h2 – ρ1h1
Concept of Buoyancy
Buoyancy is also known as buoyant force. It is the force exerted on an object that is wholly or partly immersed in a fluid. This is an important concept for eh NAT based questions that may be asked in the GATE ME exam.
Concept of Buoyancy: When a body is immersed in a fluid, an upward force is exerted by the fluid on the body, equal to the weight of the fluid displaced by the body. This acts as upward.
Archimedes’ Principle: It states when a body is immersed completely or partially in a fluid, it is lifted up by force equal to the weight of the fluid displaced by the body.
Buoyant force = Weight of fluid displaced by the body
The buoyant force on the cylinder =Weight of fluid displaced by the cylinder
VSx Value of immersed part of solid or Volume of fluid displaced
FB = pwater × g × Volume of cylinder immersed inside the water
=πpwgd2/4 (∴ w = mg pVg)
Principle of Flotation: According to this principle, if the body’s weight equals buoyant force, then the body will float.
FB = mg
VSxplg = Vspsg
pwgd2xπ/4 = pcylinder gd2hπ/4
pwx = pcylinderh
- The factors that affect buoyancy are the density of the fluid, the volume of the fluid displaced, and the local acceleration due to gravity.
- The buoyant force is not affected by the mass of the immersed object or the density of the immersed object.
Centre of Buoyancy: The point at which the force of buoyancy acts is called the center of buoyancy. It lies on the center of gravity of the volume of fluid displaced or the center of gravity of the part of the body inside the water. Point B is the center of buoyancy.
Buoyancy on a submerged body
- The Archimedes principle states that the buoyant force on a submerged body is equal to the weight of the liquid displaced by the body and acts vertically upward through the centroid of the displaced volume.
- Thus the net weight of the submerged body (the net vertical downward force experienced by it) is reduced from its actual weight by an amount that equals the buoyant force.
Buoyancy on a partially immersed body
- According to Archimedes’ principle, a partially immersed body’s buoyant force is equal to the displaced liquid’s weight.
- Therefore, the buoyant force depends upon the fluid’s density and the body’s submerged volume.
- The buoyant force must balance the body’s weight for a floating body in static equilibrium and without any other external force.
Metacenter of a Floating Body: If a body floating in liquid is given a small angular displacement, it oscillates about some point M. This point is called the metacenter.

The equilibrium of a submerged body in a liquid requires that its weight acting through its center of gravity be colinear, with equal hydrostatic lift acting through the center of buoyancy. Let us suppose that a body is given a small angular displacement and then released. Then it will be said to be in the distance MG is called metacentric height (it is the distance between the gravity center and metacenter)
Condition of Stability of Submerged Body
It is classified into three groups.
- Stable Equilibrium: When the center of buoyancy lies above the center of gravity, the submerged body is stable.
- Unstable Equilibrium: When B lies below G, the body is in unstable equilibrium.
- Neutral Equilibrium: When B and G coincide, the body is in neutral equilibrium.
Stability of Floating Bodies: When the body undergoes an angular displacement about a horizontal axis, the immersed volume’s shape changes, so the center of buoyancy moves relative to the body.
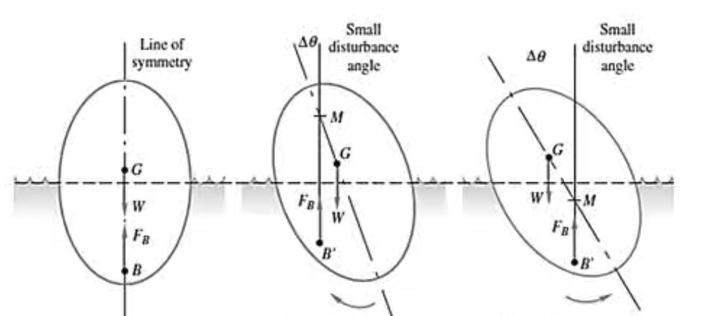
- Stable Equilibrium: When a body is given a small angular displacement by external means, and if the body comes to its original position due to internal forces, it is called stable equilibrium. It occurs when the metacenter lies above the center of gravity.
- Unstable Equilibrium: In the above case, if the body does not come to its original position and moves further away, it is known as unstable equilibrium. M lies below the center of gravity.
- Neutral equilibrium: When a body is given a small angular displacement and sets on a new position, it is called neutral equilibrium. In this, M and G coincide.
The relation between B, G and M can be expressed as GM = I/V – BG
Here, l = Least moment of inertia of the plane of the body at the water surface.
Where, I = min(Ixx, Iyy)
Ixx = bd3/12 and Iyy = db3/12
G = Centre of gravity
B = Centre of buoyancy
M = Metacentre

V is the volume submerged inside the water and can be given as V = bdx
Where b,d and x are the length, width and depth of the section or body.
- BG is the distance between the center of gravity and the centre of buoyancy. (In other words, BG = distance between the center of gravity of the whole body and the center of gravity of the submerged part of the body)
- When we find out GM, then we can determine the status of the body as
- GM > 0 (stable equilibrium),
- GM < 0 (unstable equilibrium),
- GM = 0 (neutral equilibrium).
If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE.
Online Classroom Program for ESE/GATE CE
You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams.



