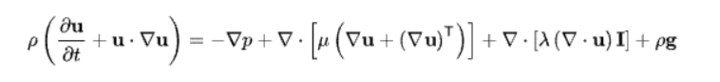- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Euler’s Equation of Motion
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Euler’s Equation of Motion in classical Mechanics extends Newton’s laws of motion for point particles to rigid body motion. Leonhard Euler developed them around 50 years after Isaac Newton developed his laws. Fluid dynamics is a highly quantitative discipline that necessitates close attention to the physical interpretations of differential equations.
Euler’s equation of motion is among the simplest to apply of all the equations used in fluid dynamics, especially in the ranges where a fluid’s viscosity and compressibility are minimal. Since they can yield intuitive results and are simpler to work with than the complete Navier-Stokes equations for compressible fluids, Euler’s equation of motion in fluid dynamics is typically used as the foundation for CFD classes. In this sophisticated area of mathematics, Leonhard Euler and the complex numbers used in these Euler equation components often work with both exponential and differential equations to create various fluid and fluid element requirements.
Table of content
Euler’s Equation of Motion
Euler’s equation of motion for a steady flow of an ideal fluid along a streamline is a relationship between a flowing fluid’s velocity, pressure, and density. It is based on Newton’s Second Law of Motion, which asserts that linear momentum is preserved without an external force. The Bernoulli equation is obtained by integrating it and converting it to energy per unit weight of the following fluid.
Formulas for GATE Mechanical Engineering – Strength of Materials
Assumptions in Euler’s Equation of Motion
Euler’s Equation of Motion is based on the following assumptions:
- The substance isn’t viscous (i,e., the frictional losses are zero).
- The substance is uniform and incompressible (i.e., the mass density of the fluid is constant).
- Continuous, steady, and streamlined flow is present.
- Over the section, the flow’s velocity is constant.
- Except for gravity and pressure forces, there is no energy or force influencing the flow.
- Because no external force is applied (non-viscous flow), linear momentum is conserved.
What are Euler’s Equations in Fluid Dynamics?
Euler’s equation of motion is the equation of motion and continuity that deal with a purely theoretical fluid dynamics problem known as inviscid flow. Although some very low-viscosity incompressible fluids, like water or alcohol, can be addressed in specific flow regimes, Euler’s equation of motion real fluids are nevertheless viscous.
Eulers Equation of Motion PDF
Due to this, Euler’s equations describe an ideal situation where fluid drag and energy dissipation are low, which is nonphysical and cannot occur in the real world. To approach Euler’s equation of motion, we can estimate the Navier-Stokes equations with extremely low viscosity.

Derive Euler’s Equation of Motion
We shall simply consider gravity and pressure forces in Euler’s equation of motion. Other factors will be ignored.
Assumptions:
As stated here, the following presumptions are the foundation for Euler’s equation of motion.
- The fluid has no viscosity. Frictional losses won’t exist at all.
- The substance is uniform and incompressible.
- The fluid moves steadily, continuously, and in a streamline.
- The section’s fluid flow velocity is consistent.
- Only the forces of gravity and pressure will be considered.
Imagine a fluid moving from point A to point B, and consider a very small cylindrical portion of this fluid flow with length dS and cross-sectional area dA, as shown in the figure below.
Consider the forces on the cylinder: Pressure force PdA, in the direction of fluid flow.
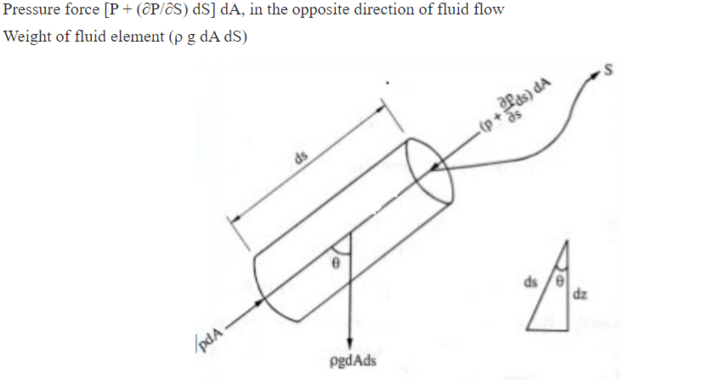
Let’s assume that the angle between the fluid flow direction and the fluid element’s weight action line is θ.
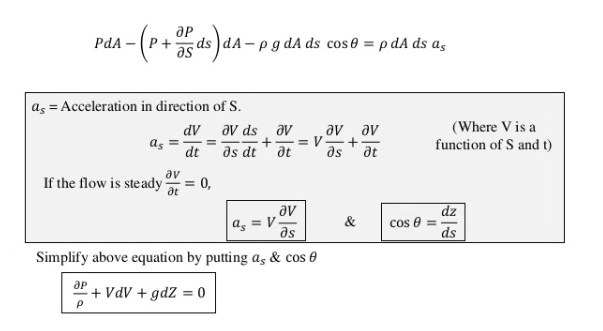
As previously stated, Euler’s equation of motion is founded on the fundamental premise of Newton’s second law of motion. As a result, we can put the following equation here:
Net force in the direction of S over the fluid element = mass of the fluid element x acceleration in the direction of S.
Inviscid Approximation
Although Euler’s equation of motion in fluid dynamics is unphysical, it can be used to describe an almost inviscid condition in which drag forces are significantly smaller than any externally applied forces. Euler’s equations can be quickly derived from the Navier-Stokes equations in this flow regime. To begin, consider the viscous terms in the Navier-Stokes equation of motion: