Kirchhoff’s Law: Formula, Diagram, PDF

What is Kirchhoff’s Law?

In 1847, Gustav Robert Kirchhoff’s introduced a pair of laws based on the law of conservation of charge and energy in an electrical circuit. The equivalent impedance of any complex network or circuit can easily be calculated using Kirchhoff’s Law.

Define Kirchhoff’s Law

The current or voltage of any circuit branch can also be calculated using Kirchhoff’s Law. These laws are valid in AC and DC networks at low frequencies.

Formulas for GATE Electronics & Communication Engineering – Digital Circuits

Types of Kirchhoff’s Law

Kirchhoff’s Law is defined based on the usage and application of the law. Kirchhoff’s laws are classified into two types:

• Kirchhoff’s Current Law (KCL)
• Kirchhoff’s Voltage Law (KVL)

Kirchhoff’s Current Law

Kirchhoff’s current law is also known as Kirchhoff’s First law or Kirchhoff’s Law of the junction, but the most used term is Kirchhoff’s Current Law or KCL. KCL is based on the law of conservation of charge.

Formulas for GATE Electronics & Communication Engineering – Electronic Devices

Define Kirchhoff’s Current Law

Kirchhoff’s current law states that the algebraic sum of currents entering a node or a closed boundary equals zero.

If there are N number of branches connected to a node and it is the current of the nth branch, then mathematically, KCL states,

^N∑_n=1i_n = 0

In this law, the current entering a node is taken as positive, and the current leaving a node is taken as negative or vice versa. Assume a set of currents ikt where k = 1, 2, 3 . . . . n flow into a node. Let i_T(t) be the total current then,

Current leaving=current entering

So, an alternate statement for KCL is that the sum of currents entering a node equals the sum of currents leaving the same node.

• Download Formulas for GATE Electronics & Communication Engineering – Control System
• Download Formulas for GATE Electronics & Communication Engineering – Digital Circuits
• Download Formulas for GATE Electronics & Communication Engineering – Electronic Devices

Application of Kirchhoff’s Current Law

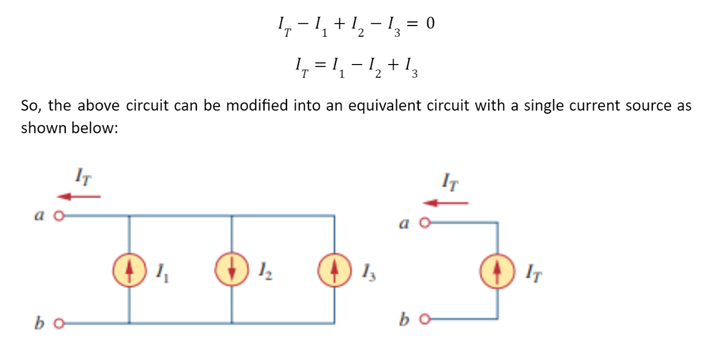
KCL is used to combine the current sources present in parallel. The overall equivalent current is the algebraic sum of individual currents present in parallel, as shown below:

Applying KCL at node a,

Validity of Kirchhoff’s Current Law

There exist some conditions where KCL is valid, and in some cases, it is not valid. Those conditions are:

• KCL is independent of the variation in temperature in the circuit.
• KCL is valid for linear, non-linear, bilateral, unilateral, passive, and active elements.
• KCL is valid for lumped electrical networks only, not for distributed electrical networks. At high frequencies, the circuit is treated as distributed and not lumped, and the effect of parasitic resistance cannot be ignored, so KCL is invalid at high frequencies.
• Kirchhoff’s law is not valid for time-varying magnetic fields.

Kirchhoff’s Voltage Law

Kirchhoff’s Voltage Law is also known as Kirchhoff’s Second law or KVL. KVL is based on the law of conservation of energy.

Define Kirchhoff’s Voltage Law

Kirchhoff’s Voltage Law states that the algebraic sum of voltages around a closed path or loop in a circuit equals zero. If there are M number of voltages in a loop and V_m is the m^th voltage, then mathematically, KVL can be written as:

^M∑_n=1v_m = 0

The sign of each voltage is taken as the polarity of the terminal encountered first as we travel around the loop. We can go around the loops in either clockwise or anti-clockwise directions. Consider the figure shown below:

This shows that KVL is based on the law of conservation of energy.

Application of Kirchhoff’s Voltage Law

KVL is used to combine the voltage sources present in series. The overall equivalent voltage is the algebraic sum of individual voltage present in series as shown below: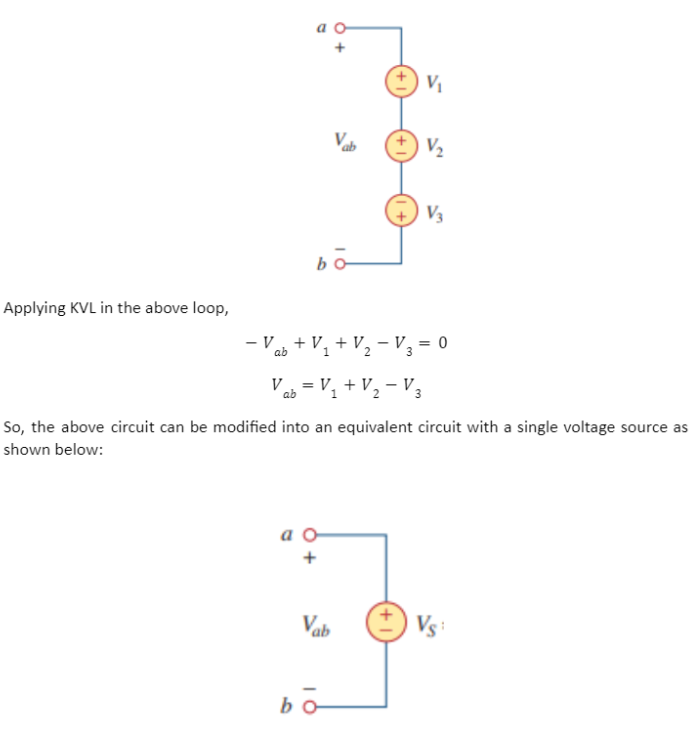

Validity of Kirchhoff’s Voltage Law

There exist some conditions where KVL is valid, and in some cases, it is not valid. Those conditions are:

• KVL is independent of the variation in temperature in the circuit.
• KVL is valid for linear, non-linear, bilateral, unilateral, passive, and active elements.
• KVL is only valid for lumped electrical networks, not for distributed electrical networks.

Validity of Kirchhoff’s Law

Kirchhoff’s Laws are valid for lumped networks, not for distributed networks. There are some hypothetical cases where KCL and KVL are not satisfied.

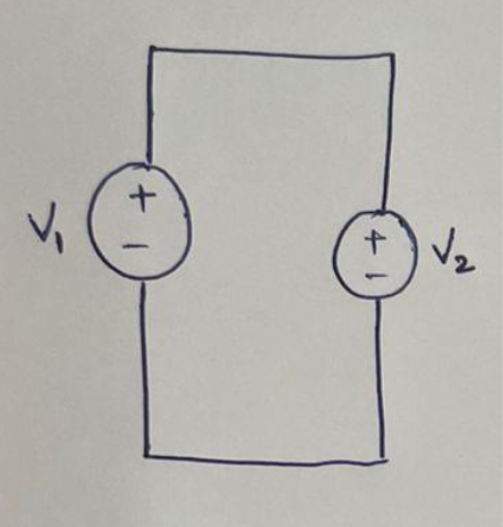
• Two unequal voltage sources are placed parallel to each other.

If V₁ ≠V₂, then the KVL violates because KVL states that the sum of voltages in a closed loop must be zero.

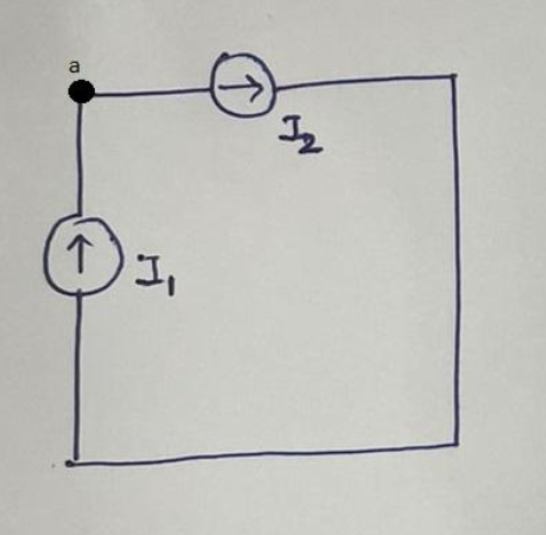
• Two unequal current sources are placed in series to each other.

If I₁ ≠I₂, the KCL violates because the current entering at node a will not be equal to the current leaving at node a.

Kirchhoff’s Law Formula

Kirchhoff’s law comprises KVL and KCL. KVL states that the algebraic sum of voltages around a closed loop equals zero. KCL states that the algebraic sum of currents entering a node is equal to zero. Mathematically, KCL and KVL can be written as:

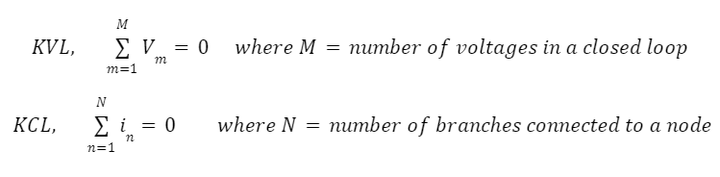
Kirchhoff’s Law Examples

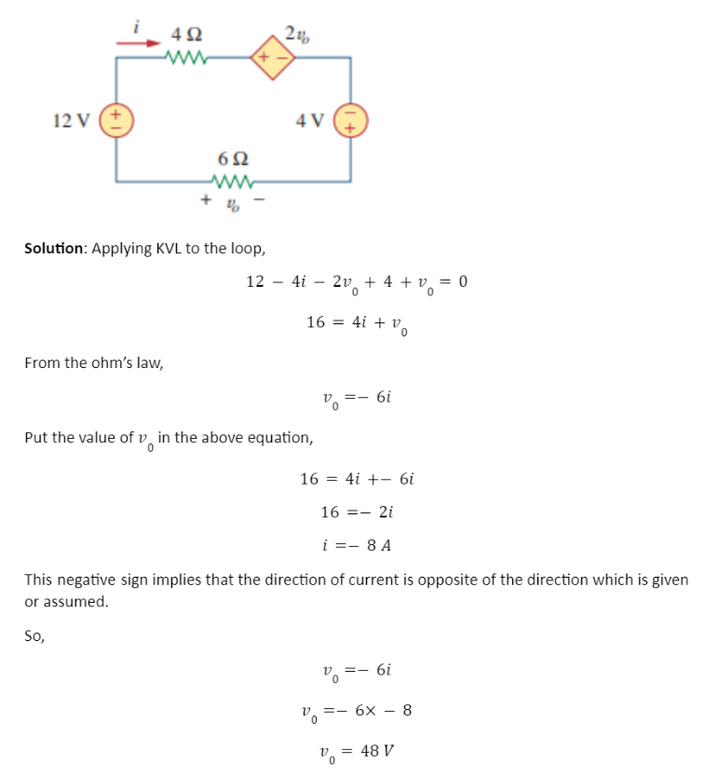
Example 1: Find current i₀ and voltage v₀ in the circuit shown below

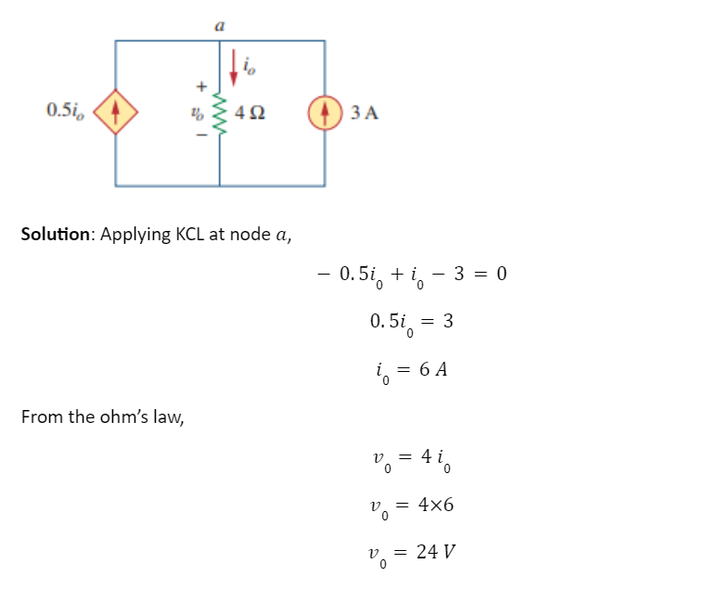
Example 2: Find current i₀ and voltage v₀ in the circuit shown below

Example 3: Determine current i and voltage v₀ in the circuit shown below

Important Topics for Gate Exam
2s Complement	Acid Propertiesn Dbms
Angle of Contact	Asynchronous Counter
Belt Drive	Bending Moment
Bending Stress	Boolean Theorems
Boundary Layer	Bresenham Line Drawing Algorithm