Slope Deflection Equation
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Slope Deflection Equation is the equation in civil engineering structural analysis based on the slope and deflections of members in a structure. Slope deflection equations are used to analyze a structure before its design. These equations are used in the slope deflection method of structure analysis, which is a method of analysis of indeterminate structures.
The structure analysis method uses the slope-deflection equation to find the structure’s unknown parameters, like rotations and moments. The main purpose is to determine the end moments of each structure member. It converts the unknowns in terms of the function of the degree of freedom of members. Slope deflection equations can be applied to all joints at equilibrium conditions. These unknowns can be determined by solving the slope deflection equations associated with the members.
Download Formulas for GATE Civil Engineering – Structural Analysis
Table of content
What is Slope Deflection Equation?
The slope deflection equation gives the relationship between end moments and the rotation of the member. A member’s rotation, deflection, and end moments are the design’s main unknown parameters in the structural analysis. The slope-deflection equations can be obtained using the superposition principle by considering separately the moments developed at each support due to each displacement θA, θB, and Δ and the loading. These equations, later modified based on the requirement of analysis, are known as the modified slope deflection equations. The modified slope deflection equations are used in formulating questions in the GATE question paper.
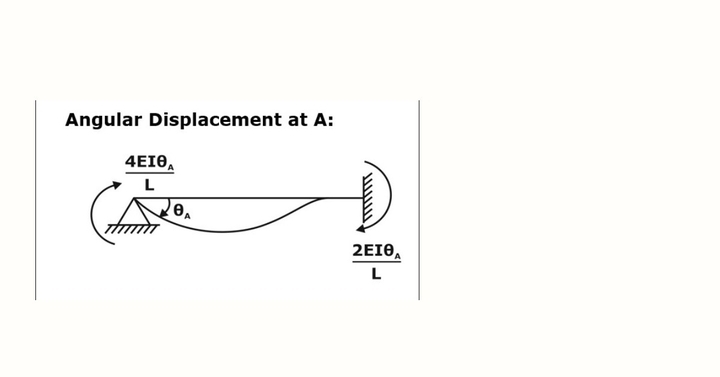
Slope Deflection Equation Derivation
Slope deflection equations are very useful for the view of structural analysis. These equations are used in the slope deflection method of analysis of indeterminate structures. The derivation of slope deflection equations is subjected to the actual problem statement, and that can be derived by considering the fixed end moments and rotation of different support conditions, which are given below:
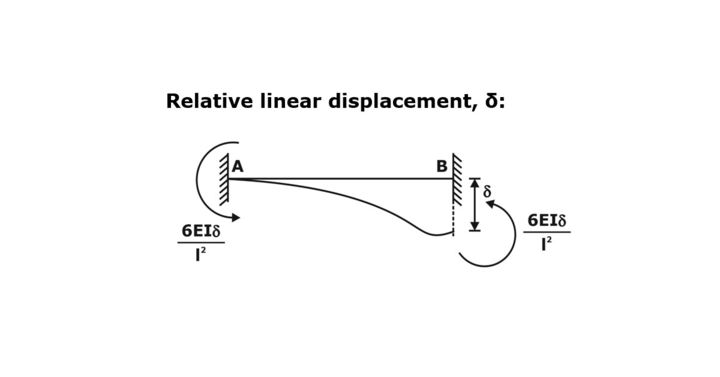
The Relative Linear displacement is shown below in the figure, which is denoted by the delta (δ)
Download Formulas for GATE Civil Engineering – Geotechnical Engineering
Slope Deflection Formula
Slope deflection formulas are based on slope deflection equations, which analyze indeterminate structures. These equations are based on some special equations and equilibrium conditions. And moments and rotations can find out by solving these equations simultaneously. Slope deflection formulas are an essential part of the GATE CE syllabus. These formulas are derived based on considering the following sign conventions:
(i) Clockwise moment is taken as positive.
(ii) If δ gives clockwise rotation to a member, it is considered positive.
With the help of the superposition principle, the slope deflection equation can be written as

Slope Deflection Equation for Continuous Beams
Continuous beams have more than two support; hence, the number of support reactions will be more than the number of available equilibrium equations. So such beams are indeterminate and can be analyzed with the help of slope deflection equations. This can be understood with the help of the following example:

As shown in the above figure, a continuous beam is given with load distributed at Points A, B, C, and D. These equations are calculated by the Slope deflection equations, which is important as per the GATE exam and calculating the bending moments at AB, BC, and CD separately.
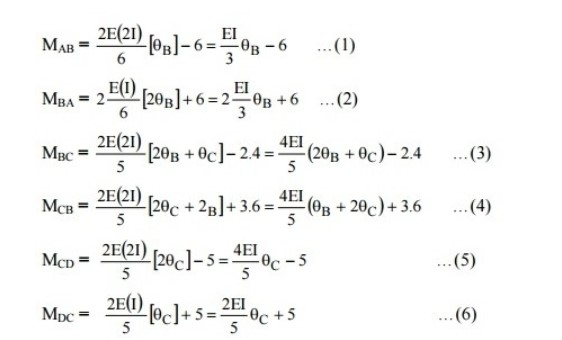
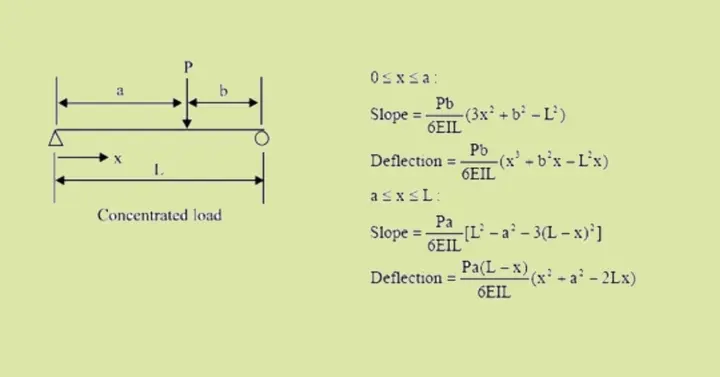
Slope Deflection Equation for Simply Supported Beam
A simply supported beam is supported by hinge support at one end, and roller support supports another. Simply supported beams can be analyzed with the help of equilibrium equations alone; hence, such a beam is determinate. Slope deflection equations can be used to determine the slope and deflection of beams under the action of external loading. This can be understood with the help of the following example:
Download Formulas for GATE Civil Engineering – Geomatics Engineering