Statically Indeterminate
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In solid mechanics, a Statically Indeterminate structure can be said if the equilibrium equation is insufficient for finding the structure’s unknowns. These unknowns can be the Deformation, Support reaction, Shear force, Bending moment, etc. For analyzing such a structure, there is a need for some special equations called compatibility equations.
In Civil engineering, the design of structures can classify into stable structures and unstable structures. An unstable structure is also called a mechanism and can not be used in civil engineering design. A structure that can be useful from a civil engineering point of view is only a stable structure, whether a statically indeterminate or a statically determinate structure.
Table of content
Statically Indeterminate Structures
A useful stable structure can be either statically determinate or indeterminate structures. In a statically indeterminate type of structure, more stress functions are available than the equilibrium equations. Such a structure needs some compatibility conditions for its analysis.
Statistically Indeterminate PDF
A statically indeterminate structure provides more stability to the structure because it has more support reactions which are called redundant reactions. Such type of structure remains in stable conditions till all the redundant reactions are present. If all the redundant reactions are removed from the structure, it will become a statically determinate structure that is just stable. In civil engineering, structures can be Beams, Frames, Trusses, Columns, etc. Here some of the statically indeterminate structures are described, which helps to understand indeterminate structures.
Statically Indeterminate Beams
Beams are structure member that resists the effect of transverse load acting over them. A beam can withstand the bending and shear effects caused by external loading. Loading can be a form of point loading, uniformly distributed loading, uniformly varying loading, or a combination of these types. Based on the support conditions and loading over the beams, it can be classified as a statically determinate beam or a statically indeterminate beam.
Statically indeterminate beams are the beams that require compatibility conditions along with available equilibrium equations for their analysis. Compatibility conditions of beams depend on the support conditions and type of loading etc. Compatibility conditions are based on the internal structure of the beams, like deformations and slopes of the beam.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Compatibility Conditions of the Indeterminate Beams
In the case of indeterminate beams, compatibility conditions are required for their analysis. Here few conditions are given which help to understand compatibility conditions
- At fixed support of the beam slope and deflections are zero
- At the hinge or roller support of the beam, only deflections are zero
- In the case of symmetric loading over a symmetric beam, the deflection will be maximum at the midpoint of the beam, and the slope will be zero at these points.
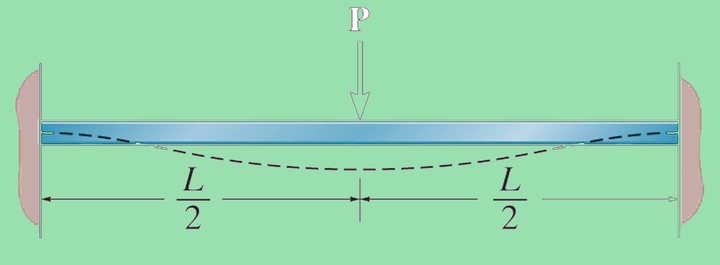
Statically Indeterminate Truss
Trusses are the member of a structure which can resist only axial loading. A truss can not withstand a bending type of load, but it can resist the shear effect caused by external loading with the help of a diagonal member of a truss. Loading over the truss can be applied only at the joints of the truss in the form of point loading. Based on the support conditions of a truss, it can be classified as a statically determinate truss or a statically indeterminate truss.
A statically indeterminate truss is a truss that requires compatibility conditions along with the available equilibrium equations for their analysis. The compatibility conditions of a truss depend on the support conditions etc. Compatibility conditions are based on the internal structure of the trusses, like deflections of joints in the truss.
Download Formulas for GATE Civil Engineering – Fluid Mechanics
Degree of Static Indeterminacy of Structures
The degree of indeterminacy of a structure can be calculated as the number of redundant reactions present in the structure. It can be classified as static indeterminacy and kinematic indeterminacy. The degree of static indeterminacy is the number of support reactions over the available equilibrium equations. The degree of kinematic indeterminacy of a structure is associated with the degree of freedom of the structure.
As we know, redundant reactions are available in statically indeterminate structures, so the degree of static indeterminacy will be more than zero. No redundant reactions are available in the case of statically determinate structures, so the degree of static indeterminacy will be zero. Statically indeterminate structures are more stable as compared to determinate structures. If the degree of indeterminacy is less than zero, such a structure is called an unstable structure or a mechanism.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Difference Between Statically Determinate and Indeterminate Structures
In the real world of civil engineering construction works, both statically determinate and indeterminate structures are used because of their suitability and requirement of the construction site. Although both types of structures have many similarities, like both are stable structures, there are also some differences between them, which are explained below.
|
Statically Determinate Structures |
Statically Indeterminate Structures |
|
The degree of indeterminacy of such structures is zero |
The degree of indeterminacy of such structures is more than zero |
|
There are no redundant reactions available in such types of structures |
There are at least one redundant reaction available in such type of structures |
|
Such structures are just stable ; |
Such structures are stable until all redundant reactions are removed |
|
For analysis of such type of structures, only equations of equilibrium are required |
For analysis of such types of structures, compatibility conditions along with equations of equilibrium are required |
|
ILD for such structures is a linear curve |
ILD for such a structure is a non-linear curve |
Statically Indeterminate Beams Examples
Statically indeterminate beams are mostly used in construction because it provides more stability to the whole structure. As we know, redundant reactions are available in statically indeterminate beams, so the degree of indeterminacy of such beams is greater than zero. A few examples of such beams are explained below:
- Fixed beam: This is a statically indeterminate beam with a fixed support at both ends. The degree of static indeterminacy of a fixed beam in the case of inclined loading is three, and in the case of vertical loading degree of static indeterminacy will be equal to two only as, in this case, the horizontal equilibrium equation is worthless.
- Propped cantilever beam: It is also a statically indeterminate beam that has fixed support at its one end, and another end of this beam is supported by either roller support or hinge support.


