Moment of Inertia
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Moment of Inertia is an important concept of Physics which is used in the domain of designing structures and designing of machines. It is important in designing because with the help of Moment of Inertia, most strongest section and most weakest section can be determined.
The moment of inertia is also known as the second moment of the area of the body about its centre of gravity. Moment of inertia measures the rotational resistance of the body. A high Moment of Inertia shows the higher rotational resistance of the body.
Download Formulas for GATE Civil Engineering – Solid Mechanics
Table of content
What is Moment of Inertia?
Moment of Inertia (MOI) is the resistive capacity of a body against its angular acceleration. Moment of inertia can be expressed as; I=mk2 where m is the mass of the body and k is the radius of gyration.
Moment of Inertia Definition
Moment of Inertia is a quantity which expresses the body’s tendency to resist external angular acceleration, which can be calculated as the sum of the products of the mass of each particle of the body with the square of its distance from the axis along which it is to be rotated.
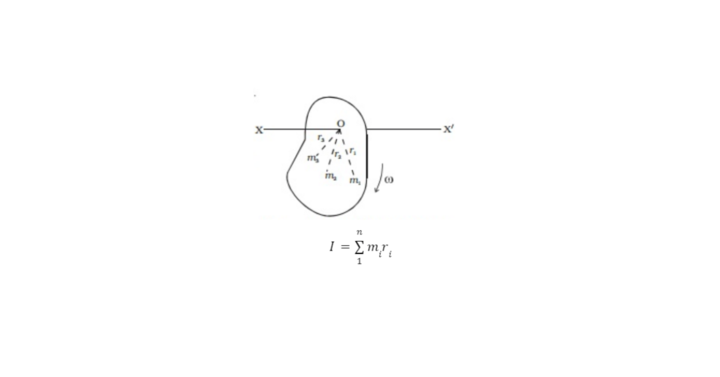
Download Formulas for GATE Civil Engineering – Fluid Mechanics
Moment of Inertia Formula
The moment of Inertia is the resistive capacity of a cross-section in rotation. The moment of inertia is also known as second-moment area which can be represented by nΣ1Aiyi where y is the distance of CG of the area from its axis
Moment of inertia can also be expressed as I=p/ω where p is the angular momentum and ω is the angular velocity of the body.
Moment of inertia can also be calculated by I=L/ω
Where, I= moment of inertia
L= angular momentum
ω= angular velocity
Unit of Moment of Inertia
As we know, I=mk2
So, the unit of Moment of inertia is kg-m2
Download Formulas for GATE Civil Engineering – Environmental Engineering
Physical Significance of Moment of Inertia
Moment of Inertia is a very important topic of physics which needs to be understood before applying it to any real-life problems. The moment of inertia of a body in rotational motion is as important as the mass of the body in its translation motion. The moment of inertia is the property of a section which shows its capacity against rotational motion.
The moment of inertia of a cross-section shows the rotational resistance of the body which depends on the distance of accumulation of mass over the cross-section. Moment of inertia tells about the cross-sectional property of a body.
Moment of Inertia of Solid Sphere
Moment of inertia of a solid sphere represents its inherent inertia which provides resistance against angular motion. The moment of inertia depends upon the distribution of mass and it is more if mass distribution is more away from its axis of rotation.
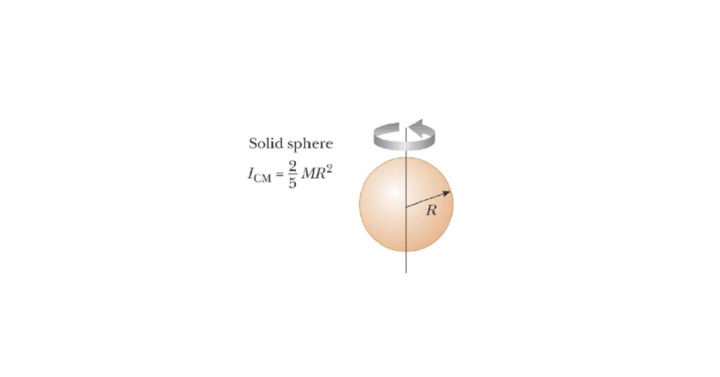
Moment of Inertia For Different Shapes
Moment of inertia for different shapes depends on the location of mass from the centre of the body. As the location of mass from the centre of body increases, its moment of inertia about its center increases which makes the section to more stronger.
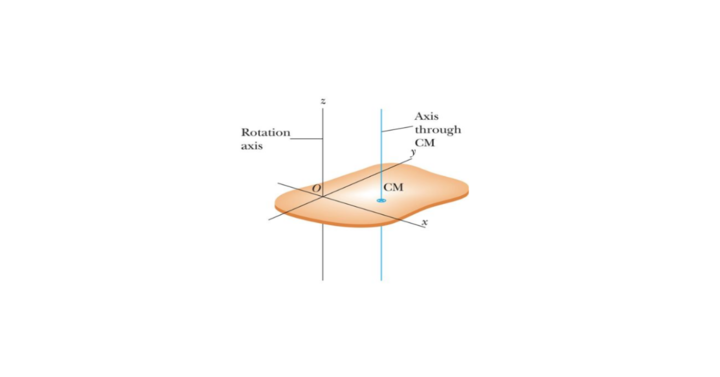
Parallel Axis Theorem
Moment of Inertia of a cross-section depends upon the axis about which the cross-section is rotating. So, if the Moment of Inertia is known about its center then it can be calculated about any axis by using two theorems.
Parallel axis theorem is used to calculate the moment of inertia of a rigid body about an axis which is parallel to the centroidal axis of the body
According to the parallel axis theorem: I=Ic+Mh2
Where, Ic is moment of inertia, M is the mass of the body and h is the distance between the new axis and centroidal axis.
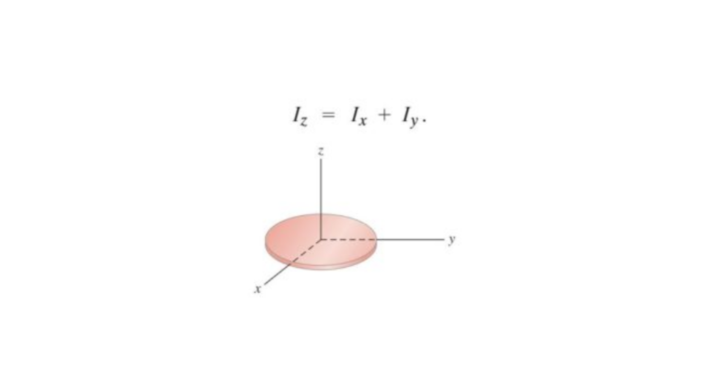
Perpendicular Axis Theorem
The perpendicular axis theorem is used to calculate the moment of Inertia of the body about the axis which is perpendicular to the plane of the body. The perpendicular axis theorem is very useful to find a polar moment of inertia and helps to find the torsional rigidity of a beam.
According to the perpendicular axis theorem; IZ=IX+IY
Effect of Rotation of Axis On Moment of Inertia
The moment of Inertia depends on the axis of rotation of the body and also depends on the distribution of mass over the entire area of the body. The moment of Inertia about a new axis of rotation x’y’ can be calculated as
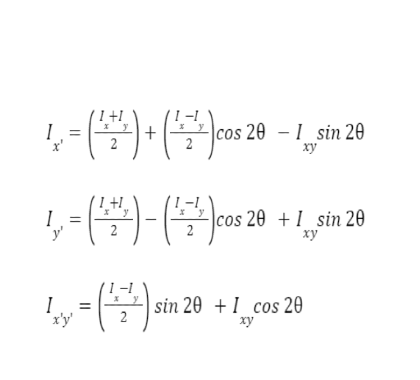
Where Ix’y’ is the product moment of inertia and θ is the rotation of the transformed axis in an anticlockwise sense.
|
Important GATE Topics |
|
| Portal Frames | Superposition Theorem |
| Binary Search Tree | Work Done By A Constant Force |
| Structural Analysis | Motion Under Gravity |
| Basic Signal Operations | Ideal Diode |


