- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Tie-Set Matrix
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Simple networks with few elements can be easily analyzed using network theorems such as Thevenin and Norton theorem, Superposition theorem, Nodal, and Mesh analysis. However, for large-scale networks with many branches, it is impossible to write a set of linearly independent equations.
The graph theory approach is a systematic and step-by-step method to analyze these large-scale networks. This article elaborates on tie set matrix definition, properties, and the procedure to find tie set matrix, KCL, and KVL equations using tie set matrix.
Table of content
What is Tie-Set Matrix
A tie-set is a set of branches in a loop such that each loop contains one link of the graph and the remaining three branches. For a graph with n number of nodes and b number of branches, the number of tie-sets equals the number of loops formed in the graph, and the number of fundamental loops equals the number of links in the graph.
Number of tie-sets = b – n + 1
Tie-set Matrix Definition
Tie-set matrix, fundamental loop matrix, or circuit matrix is represented by [B]ij and is defined as a rectangular matrix with b columns and as many rows as loops. A tie-set matrix provides the relation between branch currents and link currents. The tie-set matrix can have the following values:
- [B]ij = 1; if branch j is in the loop i and orientations coincide
- [B]ij = -1; if branch j is in the loop i and orientations do not coincide
- [B]ij = 0; if branch j is not in the loop i
Procedure to Find Tie Set Matrix
Each tree will provide an individual tie-set matrix. To write the tie-set matrix, consider a tree of the graph as shown below. The number of fundamental loops equals the number of links in the graph.
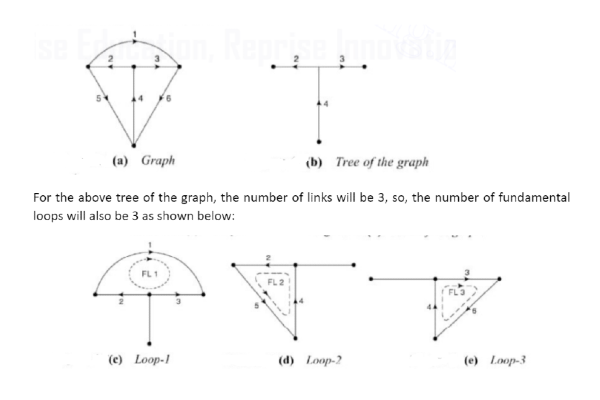
The fundamental loops represented by ‘FLn‘ and written along with the associated branches as shown below:
FL1:[1, 2, 3]
FL2:[2, 4, 5]
FL3:[3, 4, 6]
The tie-set matrix for the above example can be written as:
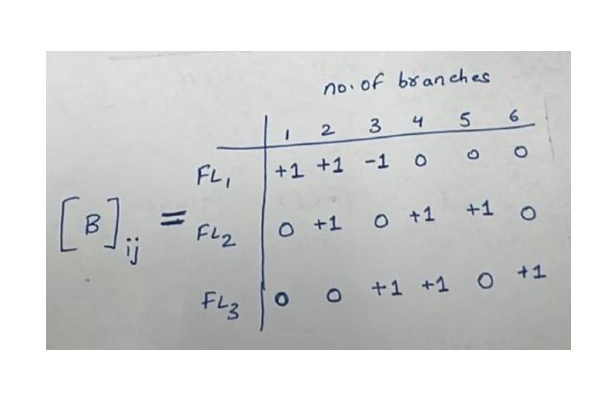
Properties of Tie set matrix
The rows of the tie-set matrix represent the fundamental loops, tie-set currents, or loop currents. The tie-set matrix column represents the tree’s number of branches. The remaining properties of the tie-set matrix are as follows:
- A fundamental loop in a tree will contain only one number of links and the remaining twigs.
- The direction of the link current present decides the orientation of the loop current in that particular loop.
- The rank of the tie-set matrix is equal to the number of tie-sets, i.e., b-n+1.
- Tie-set matrix provides the relation between loop currents and branch currents.
Tie Set Matrix and KVL
Consider the same graph and tree used in the procedure to find a tie-set matrix. Let the branch voltages be Vb1, Vb2, Vb3, Vb4, Vb5, and Vb6 of respective branches. The tie-set matrix provides the fundamental KVL mesh equations as follows:
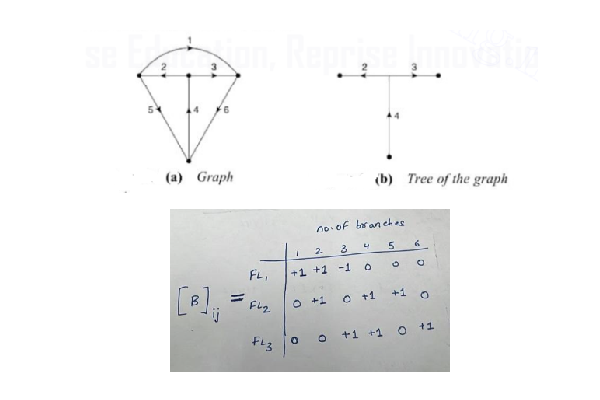
For fundamental loop 1, FL1: Vb1 + Vb2 – Vb3 = 0
For fundamental loop 2, FL2: Vb2+ Vb4+ Vb5 =0
For fundamental loop 3, FL3: Vb3 + Vb4 + Vb6 =0
The above equations can be written in matrix form as,
[B]ij [Vb]=0
Tie Set Matrix and KCL
Tie-set matrix is also used to write down the KCL equations. Consider the same graph and tree used for KVL equations as shown below. The branch currents Ib1, Ib2, Ib3, Ib4, Ib5, and Ib6 can be represented in terms of the fundamental loop currents iL1, iL2, and iL3, as shown below:
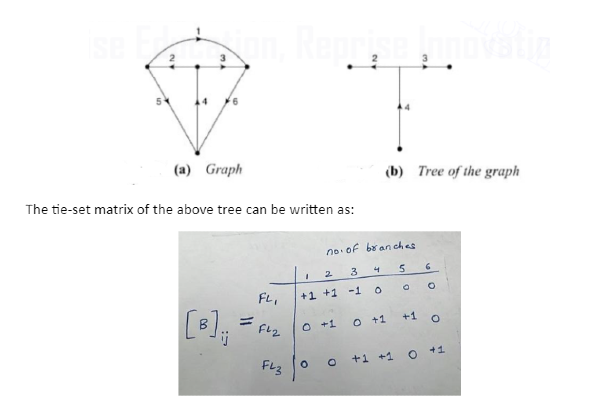
From the matrix column,
Ib1= iL1
Ib2 = iL1 + iL2
Ib3 = – iL1 + iL3
Ib4 = iL2 + iL3
Ib5 = iL2
Ib6 = iL3
In matrix form, the above equation can be written as,



