Queuing Theory Study Notes for Mechanical Engineering

Characteristics of queuing model

 

 

 

 

 

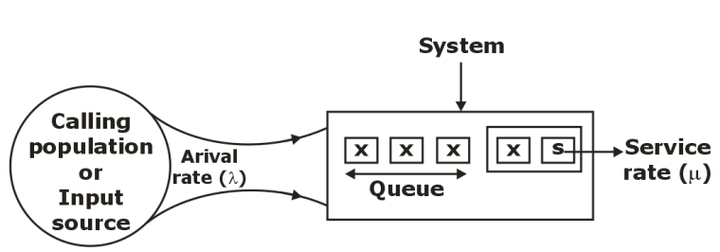
Arrival rate / Arrival Pattern: The no. of customers arriving per unit time is termed as arrival rate. Customer arrival is random & therefore it is assumed to follow the Poisson distribution.

Service Rate or Service Pattern (μ): The no. of customers serviced per unit time is known as service rate and it is assumed to follow exponential distribution (negative exponential).

 

 

 

 

 

 

Service Rule or Service Order:

It gives information about the queue discipline which means the order by which customers are picked up from the waiting line in order to provide service. E.g.

(1). FIFO or FCFS: First Come first out or First come first served

(2). LCFS: Last come first served

(3). SIRO: Service in random order

(4). Priority treatment.

System and Calling population:

System: It is the place or facilities where the customers arrive in order to get service and its capacity may be finite or infinite.

Calling population: In the entire sample of customers from which few visit the system is termed as calling population.

 

 

 

 

Customer Attitude

•  Jockeying: Customer keeps on changing queue in the hope to get service faster.
• Baulking: Customer does not join the queue & leave the system without joining as the queue is very long.
• Reneging: Customer joins the queue for a short duration & then leave the system as the queue is very slow.
• Cheater: Customer takes illegal means like fighting, bribing, etc. in the hope to get service faster.

Representation of queuing model

Queuing model is represented in Kendall & Lee notation whose general form is

 

 

Where a: probability distribution for arrival pattern

b: probability distribution for service pattern

c: no of server within the system

d: service rule or service order

e: size or capacity of the system

f: size or capacity of calling population or input source.

(i) If λ > μ:

Queue length will keep on increasing and after a certain period of time the incoming population will not get serviced. In this condition, we can’t find the solution as the system ultimately fails.

(ii). If λ < μ → System works

λ < μ → prefer

• The ratio of arrival to service rate indicates the % time server is busy it is known as utilization factor or avg. utilization or system utilization or channel efficiency or cleaning ratio.
• It also indicates the probability that a new customer will have to wait.

The probability that the system is idle or Prob. of zero customers in the system.

 

Probability of having exactly ‘n’ customer in the system

Avg. no. of customers in the system:

In these we include both the customers waiting in the queue along with those getting service.

Avg. no. of customers in the queue

In these, we do not include the customer getting serviced

Avg. waiting time of customers in the queue

The mean waiting time in queue is given by

 

Avg. waiting time of customers in the system

The mean waiting time in the system is given by

Inter-Arrival Time

The probability density function for Inter arrival time

P(t) = λ . e^–λt.

Little’s Law

 For a stable system avg, no of customers in the system or queue is given by

W_s: avg. waiting time of customer in the system

W_q: avg. waiting time of customer in the queue.

Some Important Formulae

Avg. length of non-empty queue or Avg. length of queue containing at least one customer

Probability of ‘n’ arrival in the system during period T

Probability that more than T time period is required to service a customer

 The probability that the waiting time in the queue is greater than ‘T’

The probability that the waiting time in the system is greater than T

 This topic is important for GATE ME, ISRO ME, ESE IES ME, and other Mechanical exams.

 

If you are preparing for ESE/ GATE or other PSU Exams (Mechanical Engineering), then avail Online Classroom Program for ESE and GATE ME: 

Comprehensive Preparation for GATE & ESE ME Exams(500+ Hours of Live Classes, 300+ Quizzes for Practice and 60+ Mock Tests)

You can avail Test Series specially designed for all Mechanical Engineering Exams:

Get Unlimited Access to all 161+ Mock Tests

 

All the Best!

#DreamStriveSucceed.

Update BYJU’S Exam Prep, Best GATE exam app for Preparation