What is Lami’s Theorem?
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Lami’s Theorem associates the magnitudes of Coplanar, Concurrent and Non-Collinear forces that maintain an object equilibrium. According to Lami’s Theorem, we can relate three coplanar forces with each other with the sine of the angle. It is named after Bernard Lamy, a French Mathematician. Lami’s theorem can be used to solve a lot of real-life problems.
Lami’s Theorem PDF
Lami’s Theorem comes in handy in analyzing most mechanical and structural systems. This is used when static equilibrium is maintained between various coplanar forces. This article will discuss Lami’s Theorem Proof, Formula, derivation, use, and some examples.
Table of content
What is Lami’s Theorem?
Lami’s Theorem states that if three coplanar forces acting at a point be in equilibrium, then each force is proportional to the sine of the angle between the other two. It is an important concept in the GATE CE syllabus. According to Lami’s theorem, if forces are in equilibrium, as shown in the image, then they will be related to each other with the sin of the angle formed between them.

where A, B & C are the Coplanar forces acting at a point.
Lami’s Theorem Formula
Lami’s Theorem is related to magnitudes of concurrent, coplanar, and non-collinear forces that help to keep a body or an object in static equilibrium. The theorem is very useful in analyzing most mechanical and structural systems, and various MCQ-based questions are formulated based on this in the GATE question paper.
According to Lami’s Theorem, the formula for three coplanar forces is:
P/sinα = Q/sinβ = R/sinγ
Where P, Q, and R are the Coplanar Forces acting at a point.
Lami’s Theorem Proof and Derivation
Now, let us see how we can state and prove Lami’s Theorem. This theorem can be obtained by applying the sine rule for triangles. The proof can be checked and understood well for adequate preparation for the GATE exam. Consider three Coplanar Forces, P, Q, and R, in equilibrium acting at a point ‘O’ as shown. Now, refer to the figure below.
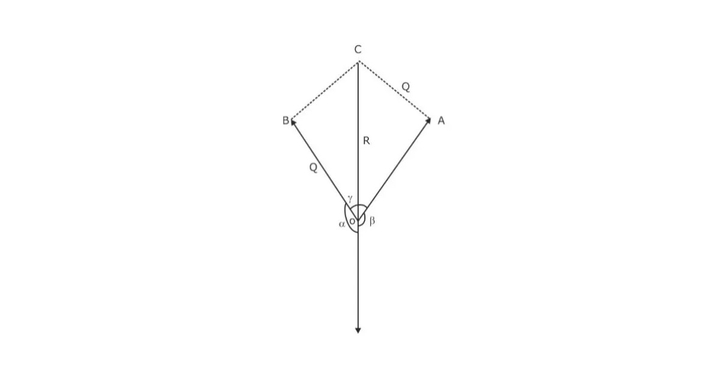
- Complete the parallelogram OACB with OA and OB as shown.
- Diagonal OC represents the resultant of two forces, P and Q.
Since these forces are in equilibrium, the resultant of the forces P and Q must be in line with OD and equal to R but in the opposite direction.
OA = P
OB = Q
OC = R
Now, α + β + γ= 360°
Angle AOC = 180° – β
Angle COB = 180° – α
Angle ACO = 180° – α (As AC is parallel to OB)
In Triangle AOC,
∠A + ∠B + ∠C = 180°
∠A + (180°-β) + (180°-α) =180°
∠A = α + β -180° ……………………………. (i)
We know that,
α + β + γ= 360°
α + β = 360° – γ
Now, in equation (i), replacing α + β by 360° –γ, we get,
∠A = 360° – γ-180°
∠A = 180° – γ
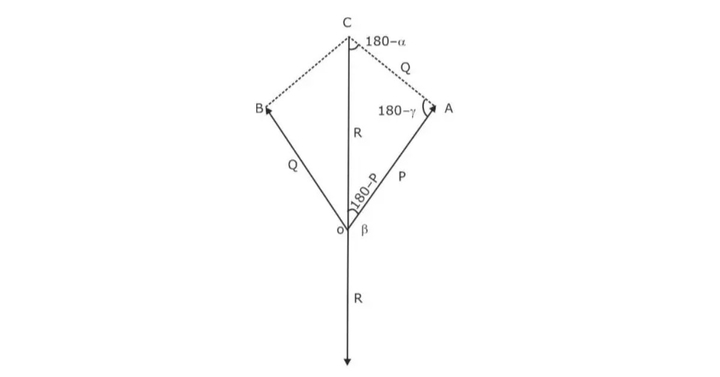
Consider Triangle AOC,
Applying Sine Rule, we get,
Limitations of Lami’s Theorem
Lami’s Theorem, though very useful, has its own limitations. As we all know, this theorem has been derived from Sine Rule for triangles; all the limitations of the Sine Rule are automatically liable to this theorem. A few limitations of Lami’s Theorem are listed below:
- It is applicable only if the body is in the State of Equilibrium of concurrent forces.
- It is not applicable for more or less than Three Concurrent Forces, which are coplanar force systems.
- It does not apply to Parallel or Non-Concurrent Force systems.
- It does not apply to Non-Coplanar Forces.
Lami’s Theorem Questions
Let us see a few of Lami’s theorem questions to understand how to apply Lami’s theorem in problems:
Question 1: A vehicle is pulled utilizing two ropes, as shown in the figure below. If the resultant pull is 1200N, find the angle and the force F. (Ans – angle = 30°, F = 1.98 kN)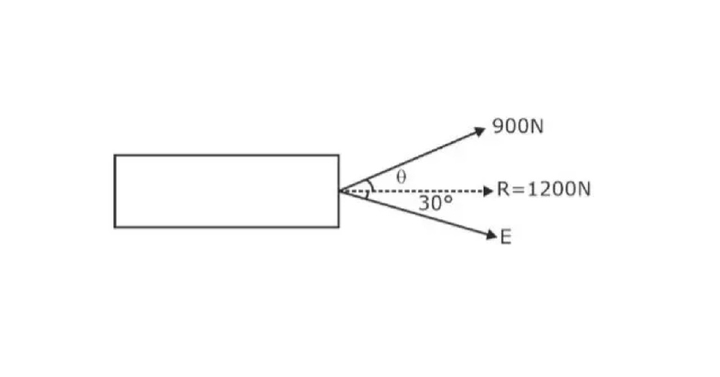
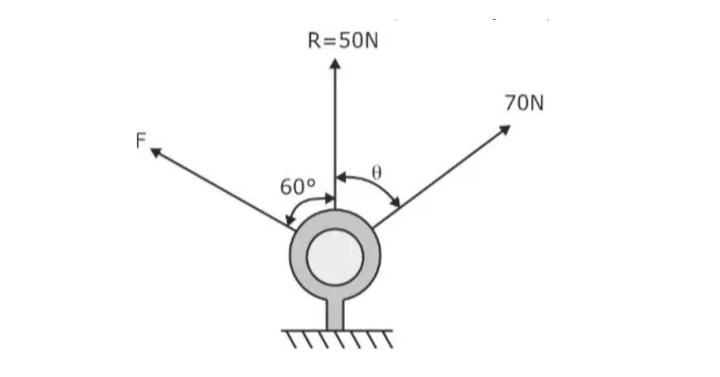
Question 2: If the resultant of Force F and 70N is R = 50kN, as shown in the figure below, find force ‘F.’ (Ans – 80N)