Kruskal’s Algorithm: Examples of Kruskal Algorithm
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Kruskal Algorithm generates the minimum spanning tree, initiating from the smallest weighted edge. Kruskal algorithm is developed for discovering the minimum spanning tree of a graph. The Kruskal algorithms are popular and follow different steps to solve the same kind of problem. This algorithm does not consider the larger problem as a whole, but the optimal solution for each smaller instance will provide an immediate output.
Before moving into the details of the Kruskal algorithm, let’s define a minimum spanning tree of a graph. A spanning tree is a subgraph of a connected, undirected graph that is structured like a tree and contains all of its vertices. As a result, a minimum spanning tree corresponds to a spanning tree with the lowest weight, where the weight of a spanning tree is the total of the weights of its edges present in it. Let us now see Kruskal Algorithm along with its working, pseudocode, time complexity of Kruskal Algorithm and a lot more in detail.
Table of content
What is Kruskal Algorithm?
Kruskal Algorithm is used to discover the smallest spanning tree of a connected graph and the spanning forest of an undirected edge-weighted graph. Basically, it accepts a graph as input and discovers the subgroup of the edges of that graph. The Kruskal algorithm follows the Greedy approach to compute the minimum spanning tree.
Kruskal’s Algorithm computes the minimum spanning tree by considering the edges in increasing order of weight. The intermediate result of the Kruskal algorithm may be a connected or disconnected graph. The Kruskal algorithm can be implemented using Union find data structure. Using the Kruskal algorithm, we can find MST in network architecture gives you the smallest length of wire required to link all the nodes (servers).
Suppose G(V, E) is a connected, weighted graph in which V is the number of vertex and E is the number of edges in the graph G. Kruskal algorithm is used to find a minimum-cost spanning tree (MCST) of a given graph G. It uses a greedy approach to find MCST because at each step it adds an edge of least possible weight to the set A.
Working of Kruskal Algorithm
Kruskal algorithm starts with the minimum single node in the graph and then explores the other minimum node at every step. Kruskal algorithm finds the subset of edges that includes the vertex of the graph such that the sum of the edges’ weights can be minimized. The working of the Kruskal algorithm is as follows:
- First, examine the edges of G in the order of increasing weight.
- Then select an edge (u, v) є E of minimum weight and check whether its endpoints belong to the same or different connected components.
- If u and v belong to different connected components, we add them to set A. Otherwise, it is rejected because it can create a cycle.
- The algorithm terminates when only one connected component remains (that is, all the vertices of G have been reached).
Kruskal Algorithm Pseudocode
The Kruskal algorithm takes an undirected connected weighted graph G(V, E), where V represents the number of vertices and E represents the number of edges in the graph. The output of the Kruskal algorithm is a minimum cost spanning tree T(V, E’) of the given graph G. Here, the V is the same as the given graph, but the E’ is changed as we do not include all the edges of the graph G. The pseudocode of Kruskal algorithm is as given below:
KRUSKAL MCST (G, W)
{
Sort the edges of E in order of increasing weight
A←Ø
for (each vertex v є V[G])
do MAKE_SET(v)
for (each edge (u, v) є E, taken in increasing order of weight)
{
if (FIND SET (u) ≠ FIND_SET (V))
A←A ∪ {(u, v)}
MERGE(u, v)
}
return A
}
Analysis of Kruskal Algorithm
Suppose G(V, E) is a connected, weighted graph in which V is the number of vertex and E is the number of edges in graph G. The analysis of the Kruskal algorithm is as follows:
- Sorting of edges requires O(|E| log |E|) time.
- Since, in any graph, the minimum number of edges is (V-1), and the maximum number of edges (when the graph is complete) is V(V- 1)/2. Hence V- 1 ≤ E ≤ V (V-1)/2. Thus O(E log E)= O(E log (V(V-1)/2)) = O(E log V)
- Initializing the n-disjoint set (in lines 3-4) using MAKE_SET will require O(V) time.
- There are at most 2 |E| FIND SET operations (since there are E edges and each edge has 2 vertices) and (V-1) MERGE operations. Thus we require O((2E+ (V-1)log n) time.
- At worst, O(V) time for the remaining operations.
- We know that E ≥ (V-1) for a connected graph.
So the total time for Kruskal algorithm is O((2E+ (V-1) logV) = O(|E| log |V])
Time complexity of Kruskal Algorithm
The time complexity of the Kruskal algorithm is O(ElogE) or O(ElogV). Sorting of edges takes O(ELogE) time. After sorting, we iterate through all edges and apply the find-union algorithm. The find and union operations can take at most O(LogV) time.
So overall complexity of the Kruskal algorithm is O(ELogE + ELogV) time. The value of E can be at most O(V2), so O(LogV) is O(LogE) the same. Therefore, the overall time complexity is O(ElogE) or O(ElogV)
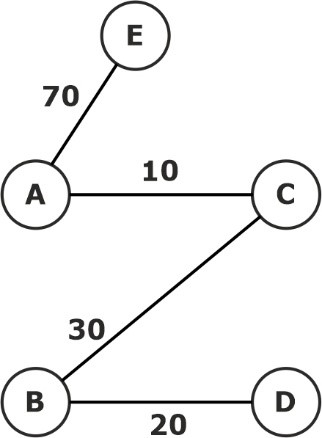
Kruskal Algorithm Example
Consider the following graph:
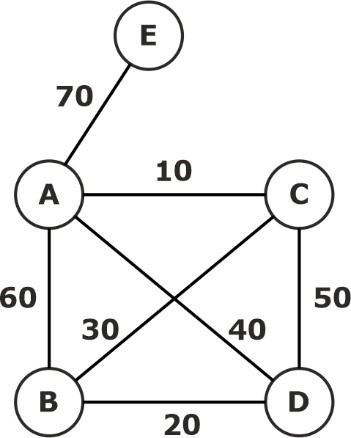
What is the minimum cost spanning tree of the above graph using the Kruskal algorithm?
Solution:
The weight of the following graph’s edges is shown in the table below:
|
Edges |
AB |
AC |
AD |
AE |
BC |
BD |
CD |
|
Weight |
60 |
10 |
40 |
70 |
30 |
20 |
50 |
Sort the edges mentioned above in increasing order of weight.
|
Edges |
AC |
BD |
BC |
AD |
CD |
AB |
AE |
|
Weight |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
We will make the spanning tree step by step,
- Choose the minimum edge that is AC
- Choose the following minimum that is BD
- Repeat the next minimum, which is BC
- Next minimum, AD, but this will create a cycle, so discard it.
- Similarly, discard the next edges CD, AB because they form a cycle.
- At last, include the edge AE.
So, the final spanning tree is: