- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Thermodynamic Relations
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Thermodynamics is the study of the relationship between heat, energy, and work. In thermodynamics, there are several fundamental laws and relationships that govern the behaviour of these quantities. Thermodynamic relations are the mathematical equations that describe these fundamental laws and relationships. Understanding these relations is essential for predicting the behaviour of thermodynamic systems and for engineering applications.
The four fundamental laws of thermodynamics are the zeroth law, the first law, the second law, and the third law. The zeroth law states that if two systems are each in thermal equilibrium with a third system, they are also in thermal equilibrium with each other. The first law, also known as the law of conservation of energy, states that the total energy of a system is conserved. The second law, also known as the law of entropy, states that the total entropy of a closed system always increases over time. The third law, also known as the law of absolute zero, states that the entropy of a perfect crystal at absolute zero is zero.
Table of content
Thermodynamic Relations
Thermodynamic relations are the mathematical expressions that relate the different thermodynamic properties of a system. For example, the equation of state relates the pressure, volume, and temperature of a gas. The Maxwell relations relate the partial derivatives of the thermodynamic properties with respect to each other. The Clausius-Clapeyron equation relates the rate of change of vapour pressure with temperature and the latent heat of vaporization.
In thermodynamics, the relationships between the different thermodynamic properties are essential for predicting the behaviour of a system. For example, these relationships are used to predict the phase transition behaviour of substances, such as the melting and boiling points. They are also used in engineering applications, such as designing heat engines and refrigeration systems. Therefore, understanding the different thermodynamic relations is essential for students and professionals in the fields of physics, chemistry, and engineering.
Maxwell’s Equations
Maxwell’s equations are a set of four equations that describe the behaviour of electromagnetic fields. These equations relate electric and magnetic fields to their sources, such as charges and currents. Maxwell’s equations are an essential part of thermodynamics, as they form the basis for understanding the behaviour of energy transfer through electromagnetic fields. They are widely used in many areas of science and engineering, including optics, electrical engineering, and communications.
Maxwell’s equations are important in the development of technologies that harness electromagnetic energy, such as radio and microwave communication, X-ray imaging, and lasers. They also provide a framework for understanding the behaviour of waves in different mediums, such as sound waves and seismic waves. These are the set of equations that establish the relation between the partial derivatives of properties P, V, T, and S of a simple compressible system.
dU = TdS – PdV
dH = TdS + VdP
Helmholtz function
F = U – TS (availability of closed system)
Gibb’s function
G = H – TS (availability of open system)
For all real processes, the value of the Helmholtz function and Gibbs function decreases and attains a min value at equilibrium.
Helmholtz function
F = U – TS (availability of closed system)
Gibb’s function
G = H – TS (availability of open system)
For all real processes, the value of the Helmholtz function and Gibbs function decreases and attains a min value at equilibrium.
Hence Four Maxwell’s relations are,
(∂T/∂V)s = – (∂P/∂S)V
(∂T/∂P)s = (∂V/∂S)P
(∂P/∂T)V = (∂S/∂V)T
(∂V/∂T)p = – (∂S/∂P)T
COEFFICIENT OF VOLUME EXPANSION (β)
β = 1/v (∂V/∂T)p
It is the rate of change of volume with respect to temperature at constant pressure.
ISOTHERMAL COMPRESSIBILITY (KT)
KT = – 1/v (∂V/∂P)T
It shows the rate of change of volume with respect to pressure at a constant temperature or at isothermal conditions.
T-dS Equation
The T-dS equation is a thermodynamic relation that describes the change in entropy of a system due to a change in temperature. It relates the change in entropy of a system to the heat transferred and the temperature at which the heat transfer occurs. The T-dS equation is a powerful tool for predicting the behaviour of thermodynamic systems and is used in a wide range of applications in physics, chemistry, and engineering.
TdS = CvdT + T(∂P/∂T)vdV
This is known as the first Tds equation
TdS = CpdT – T (∂v/∂T)TdP
This is known as the second TdS equation.
Cp – Cv = -T (∂V/∂T)p(∂P/∂V)T
T = Positive
(∂V/∂T)p = Positive
(∂p/∂V)T = Positive
Cp –Cv = +ve
Cp > Cv
Energy Equation
The energy equation is a fundamental thermodynamic relation that expresses the conservation of energy in a system. It relates to the internal energy, heat transfer, and work done in a system. The energy equation is essential for predicting the behavior of thermodynamic systems and is used in various engineering applications, such as designing heat engines and refrigeration systems.
dU = CvdT + [T(∂P/∂T)v – p]dV
Joule Thompson Coefficient (µ)
When a fluid passes through the porous plug, capillary tube, or valve, its pressure decreases. The throttling process is isenthalpic in nature. The temperature behavior of the fluid during throttling is described by the joule Thompson coefficient(µ),
µ = (∂T/∂P)h
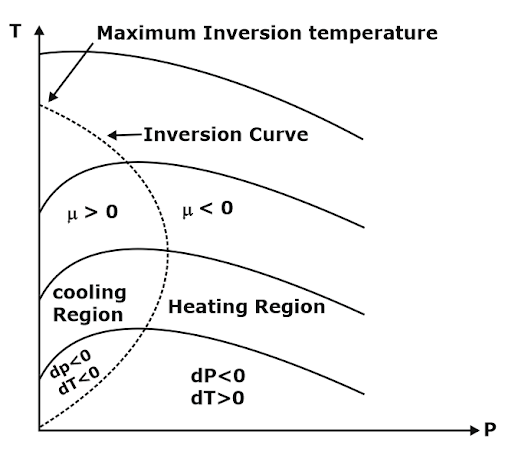
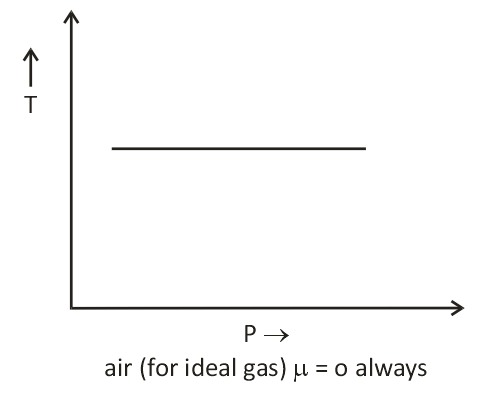
Important points:
- Joule Thomson coefficient is +ve in the cooling region i.e slope of the isenthalpic curve on the T–P diagram is +ve in the cooling region,
- μ is –ve in the heating region i.e the slope of the isenthalpic curve on the T–P diagram is –ve in the heating region,
- There is nothing as a heating or cooling region for an ideal gas the value of the joule Thomson coefficient is zero everywhere.
Clausius Clapeyron Equations
Clausius Clapeyron equation is a relationship between saturation pressure, temperature, and enthalpy of vaporization and the specific volume of two phases involved. This equation helps in the calculations of properties in two-phase regions.
sg-sf = [Latent heat (LH)]/ Tsat = [(hfg) or (hg – hf)]/ Tsat
dP/dT = (hfg)/ Tsat (vg -vf) ⇒ Clapeyron Equation
dP/dT = Psat (L.H.)/R(Tsat)2
The above equation is called the Clausius Clapeyron equation. It helps to determine enthalpy change associated with phase change by measuring pressure, temperature, and volume.



