- Home/
- GATE MECHANICAL/
- GATE ME/
- Article
Hydraulic Turbines in Fluid Mechanics
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Hydraulic Turbines are a device that converts the potential energy of water into mechanical energy. Hydraulic turbines and Hydro Machines are the section of Fluid Mechanics that deals with topics such as Turbines, pumps, and their working. This section includes all the aspects regarding applying Fluid Mechanics in the real world. The hydraulic turbine is one of the useful applications of mechanical energy.
Hydraulic Turbines PDF(Download GATE Notes)
Hydraulic turbines have been used for many years to generate electricity from renewable sources, and they continue to be an important part of the global energy mix. This article explains the best study notes on Hydraulic Turbines and Hydro Machines that are useful for Fluid Mechanics preparation for GATE and other Mechanical engineering exams.
Table of content
What is the Hydraulic Turbine?
The hydraulic turbine is one of the applications of mechanical devices, And they can be used to convert mechanical energy into electrical energy. It can be explained as follows:
- Devices used to convert hydraulic energy into mechanical energy or mechanical energy to hydraulic energy are known as Hydraulic Machines.
- The hydraulic machines used for converting hydraulic energy into mechanical energy are known as Turbines, which convert mechanical energy into hydraulic energy and are known as Pumps.
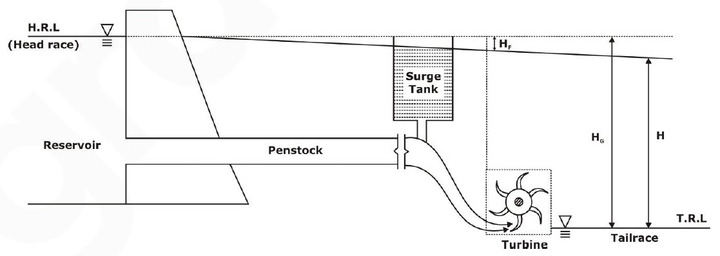
In a Hydroelectric plant, as shown above:
- A Dam is constructed across a river or a channel for storing water. The reservoir is also known as the Head race.
- Pipes of large diameter called Penstock carry water under pressure from the storage reservoir to the turbines. These pipes are generally made of steel or reinforced concrete.
- Turbines have different types of vanes, buckets, or blades mounted on a wheel called a runner.
- Tail-race is a channel carrying water away from the turbine after the water has worked on the turbines. The water surface in the tail race is also referred to as the tail race.
Important Terms of Hydraulic Turbine
- Gross Head (Hg ): Vertical difference between headrace and tailrace.
- Net Head (Hnet): The actual head available at the inlet to work on the turbine is called the Net Head. It can be mathematically expressed as Hnet = Hg – hL.
- Total Head Loss (hL): hL is the total head loss during the transit of water from the headrace to the tail race, mainly the head loss due to friction, and is given by, hf = fLV2/2gD = 4f’LV2/2gD. Where, ‘f’ is the coefficient of friction of penstock, which depends on the type of material of penstock, ‘L’ is the total length of the penstock, ‘V’ is the mean flow velocity of water through the penstock, ‘D’ the diameter of penstock and g is the acceleration due to gravity.
Types of Efficiencies
Efficiencies are classified based on the inputs and outputs parameters. Considering different forms of input and output, the efficiencies can be classified as follows:
- Hydraulic Efficiency(ηh)
- The ratio of the power generated by the runner of a turbine to the power supplied at the inlet of the turbine is known as Hydraulic efficiency.
- As the power supply is in the hydraulic form, and the possible losses occur between the striking jet and vane, it is rightly called hydraulic efficiency.
- If R.P. is the Runner Power and W.P. is the Water Power:
ηh = Runner Power/Water Power = R.P./W.P.
- Mechanical Efficiency(ηm)
- The ratio of the power available at the shaft to the power generated by the runner of a turbine is called Mechanical Efficiency.
- The runner’s energy loss in the annular area between the nozzle and spear is due to slips and other mechanical problems.
- If S.P. is the Shaft Power:
ηm = S.P./R.P.
- Overall Efficiency(ηo):
- The ratio of the power available at the shaft to the power supplied to the inlet of a turbine is termed overall efficiency.
- Because this covers the overall problems of energy losses, it is known as overall efficiency.
- It depends on both the hydraulic losses and the slips and other mechanical problems that will create a loss of energy between the jet power supplied and the power produced at the shaft available for coupling of the generator.
ηo = (S.P./R.P.)×(R.P./W.P.)
- Volumetric Efficiency
![]()
![]()
Classification of Hydraulic Turbines
Hydraulic Turbines are the equipment that converts hydraulic energy into mechanical energy. It can be classified based on different parameters.
- The hydraulic turbines can be classified based on the type of energy at the inlet, the direction of flow through the vanes, the head available at the inlet, discharge through the vanes, and specific speed.
- They are classified as:
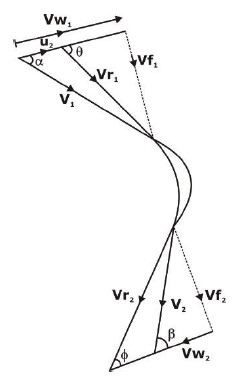
1. Pelton Turbine
- The Pelton wheel turbine is an impulse turbine. In this type of turbine, the nozzle is connected at the exit of the penstock, which converts the available energy head into a velocity head.
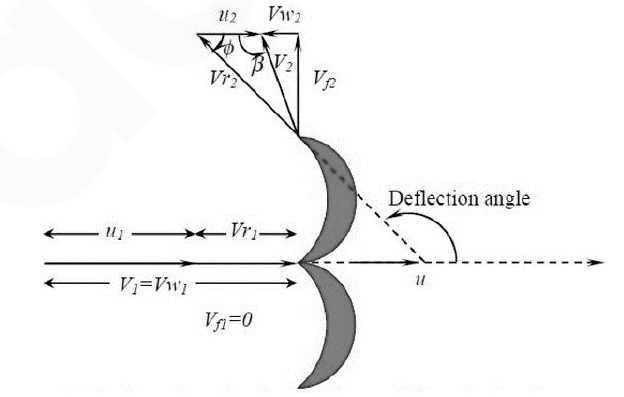
Where,
- u= wheel velocity
- V= Jet velocity
- Vr= relative velocity
- Vw=whirl velocity
- φ=Angle by the relative velocity at the outlet
- β= Guide blade angle at the outlet and u1=u2=u=2πN/60 where N= no. of rotation of the wheel
Tangential flow Impulse Turbine
Basic components of Impulse Turbine are:
- Nozzle
- Runner and buckets
- Casing
- Breaking Jet
The power is given to the Pelton turbine = ρaV1(Vw1 ± Vw2)u Nm/sec
Hydraulic efficiency is given by
ηh = [(V1 – u)(1 + kcosΦ)u](V12/2)
For maximum efficiency dηh/du = 0
(ηh)max = (1 + kcosΦ)/2
Point to Remember
- The velocity of jet: V1=CV×√(2gH) where CV=0.98 to 0.99 and called the coefficient of velocity.
- The velocity of wheel: u=φ √(2gH) where φ = Speed ratio (u/V1) (0.43 to 0.48)
- The velocity of wheel u= πDN (rps)
- Jet ratio (m) =D/d (pitch diameter ratio to jet diameter; generally 12).
- Number of bucket Z= 15+(D/2d) = 15+0.5 m
- The number of jets is the ratio of the total flow rate to the Rate of flow by a single jet.
2. Radial Flow Reaction Turbine
- In this type of turbine, the water strikes the runner, and it has both a kinetic energy head and a pressure energy head. Due to the KE head, the impulse will generate, which is similar to the case of an impulse turbine.
- Impulse: kinetic head
Reaction: Pressure head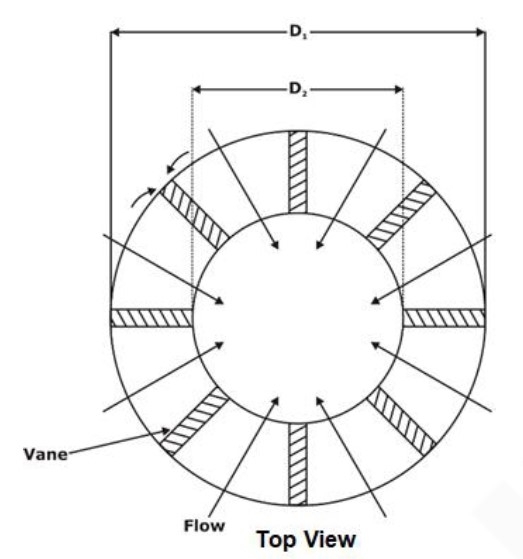
- Let B1, B2 = width of the runner at the inlet and outlet
Area of flow at inlet: A1 = πD1B1
Area of flow at inlet: A2 = πD2B2
If vane thickness is taken into consideration:
Net Area of flow = [πD1 – nt] · B1 = kπD1B1
K is a factor for the net area, and n is the number of vanes.
Q = A1Vf1 = A2Vf2
Q = πD1B1Vf1 = πD2B2Vf2
Fradial = m(Vf1 – Vf2)
Since Vf1 = Vf2
Thus Fradial should be zero
Hence, πD1B1 = πD2B2
D1B1 = D2B2
D1>D2
B1
Note: If it is given that B1 =B2, then Vf1 ≠ Vf2
3. Francis Turbine
- Francis turbine is an inward flow reaction turbine.
- To maximize runner power, V2 should be minimum. It can be done by converting the absolute velocity direction into the radial direction of the runner at the exit.
It means that
β 90°
V2 = Vf2
Vw2 = 0
Hence, R.P. = ρQVw1u1
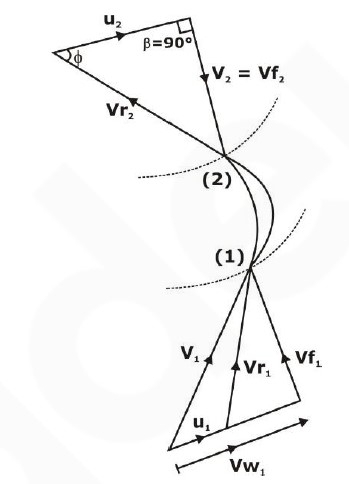
Hydraulic efficiency (ηh) = RP/HP = ρQVw1u1/ρQgH = Vw1 u1
ηh = Vw1u1/gH
4. Axial Flow Reaction Turbine
- Kaplan turbine and propeller turbines are examples of axial flow reaction turbines.
RP = m(Vw1u1 + Vw2u2)
What is Draft Tube?
The draft tube is the tube fitted at the exit location of the runner of the turbine. It is the diverging tube used to available kinetic energy at the exit of the runner.
- A draft tube is a pipe of a gradually increasing cross-sectional area, linking the runner outlet to the tailrace, and is used to discharge water from the turbine exit to the tail race.
- An end of the draft tube is linked to the runner outlet, and the other end is submerged under the water level in the tail race.
Functions
- It permits a negative head to be established at the outlet of the runner and thereby increasing the net head on the turbine.
- It converts a large proportion of kinetic energy being rejected at the outlet of the turbine into helpful pressure energy.
Specific Speed
- The value of a specific speed for a turbine is the speed of a geometrically similar turbine that would produce unit power (one kilowatt) under a unit head (one meter).
- This value is provided by the manufacturer (along with other ratings) and will always refer to the point of maximum efficiency.
Ns = N(P)0.5/H(5/4) - Specific Speed is not a dimensionless number. It dimension [M1/2L–1/4T-5/2].
Model Laws
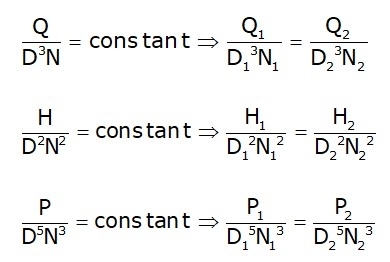
What are Centrifugal Pumps?
- A hydraulic machine that converts mechanical energy into hydraulic energy or pressure energy is known as a pump.
- A centrifugal pump (also called a Rotodynamic pump or dynamic pressure pump) works on the principle of centrifugal force.
- In Centrifugal pumps, the liquid is subjected to a whirling motion by the rotating impeller, which is made of several backward-curved vanes.
Classification of Centrifugal Pumps
centrifugal pumps can be categorized based on different parameters. These are explained as follows:
| S. No. | Classification Criteria | Types of Pumps |
| 1 | Casing design |
|
| 2 | Number of impellers |
|
| 3 | Number of entrances to the Impeller |
|
| 4 | Disposition of shaft |
|
| 5 | Liquid handled |
|
| 6 | Specific speed |
|
| 7 | Head (H) |
|
Heads on a Centrifugal Pump
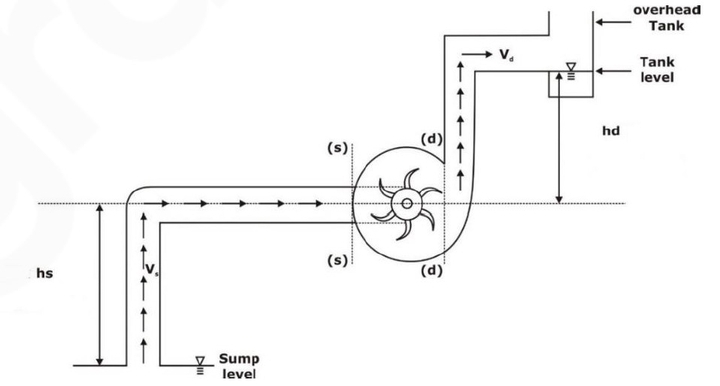
- Suction head (hs)
- It is the vertical distance between the liquid level in the sump and the center line of the pump.
- It is expressed as meters.
- Delivery head (hd)
- It is the vertical distance between the center line of the pump and the liquid level in the overhead tank or the supply point.
- It is expressed in meters.
- Static head (Hs)
- It is the vertical difference between the liquid levels In the overhead tank and the sump when the pump is not working.
- It is expressed as meters.
Therefore: Hs= (hs+ hd)
- Friction head (hf)
- It is the sum of the head loss due to the friction in the suction and delivery pipes.
- The friction loss in both pipes is calculated using Darcy‟s equation.
hf = fLV2/2gD = 4f’LV2/2gD
- Total head (H)
- It is the sum of the static head Hs, friction head (hf), and the velocity head in the delivery pipe (V2d /2g). Where, Vd=velocity in the delivery pipe.
Hm = hs +hd +hfs + hfd + Vd2/2g
- It is the sum of the static head Hs, friction head (hf), and the velocity head in the delivery pipe (V2d /2g). Where, Vd=velocity in the delivery pipe.
- Manometric head(Hm)
- It is the total head developed by the pump.
- This head is slightly less than the heat generated by the impeller due to some losses in the pump.
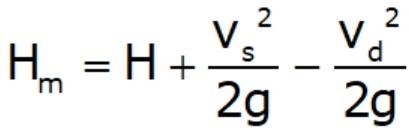
- Power of pump
(i).Power requirement of pump = shaft power (SP)
(ii). Impeller power (IP) = SP – (mechanical frictional losses)
(iii). Manometric power or output power (MP)= ρQgHm
SP > IP > MP
Applications of Hydraulic Turbine
Here are some common applications of hydraulic turbines:
- Generating electricity in hydroelectric power plants
- Providing mechanical power for industrial processes, such as milling and pumping
- Driving water pumps for irrigation and water supply systems
- Assisting in flood control and water management by regulating the flow of water in rivers and reservoirs
- Providing propulsion for ships and submarines using water propulsion turbines.


