Tie-Set Matrix

What is Tie-Set Matrix

A tie-set is a set of branches in a loop such that each loop contains one link of the graph and the remaining three branches. For a graph with n number of nodes and b number of branches, the number of tie-sets equals the number of loops formed in the graph, and the number of fundamental loops equals the number of links in the graph.

Number of tie-sets = b – n + 1

Tie-set Matrix Definition

Tie-set matrix, fundamental loop matrix, or circuit matrix is represented by [B]_ij and is defined as a rectangular matrix with b columns and as many rows as loops. A tie-set matrix provides the relation between branch currents and link currents. The tie-set matrix can have the following values:

• [B]_ij = 1; if branch j is in the loop i and orientations coincide
• [B]_ij = -1; if branch j is in the loop i and orientations do not coincide
• [B]_ij = 0; if branch j is not in the loop i

Procedure to Find Tie Set Matrix

Each tree will provide an individual tie-set matrix. To write the tie-set matrix, consider a tree of the graph as shown below. The number of fundamental loops equals the number of links in the graph.

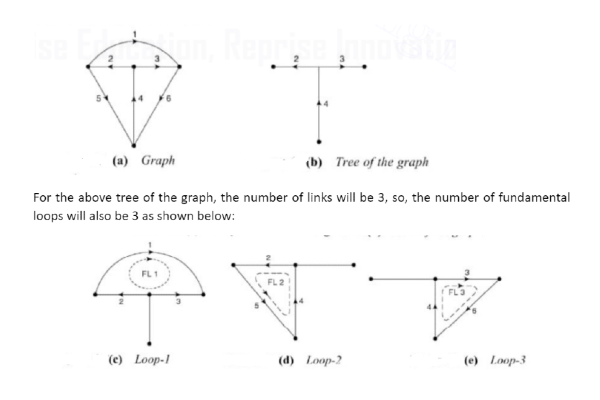
The fundamental loops represented by ‘FL_n‘ and written along with the associated branches as shown below:

FL₁:[1, 2, 3]

FL₂:[2, 4, 5]

FL₃:[3, 4, 6]

The tie-set matrix for the above example can be written as:

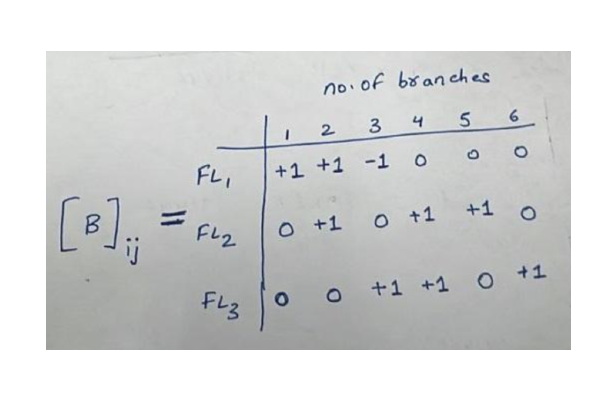
Properties of Tie set matrix

The rows of the tie-set matrix represent the fundamental loops, tie-set currents, or loop currents. The tie-set matrix column represents the tree’s number of branches. The remaining properties of the tie-set matrix are as follows:

• A fundamental loop in a tree will contain only one number of links and the remaining twigs.
• The direction of the link current present decides the orientation of the loop current in that particular loop.
• The rank of the tie-set matrix is equal to the number of tie-sets, i.e., b-n+1.
• Tie-set matrix provides the relation between loop currents and branch currents.

Tie Set Matrix and KVL

Consider the same graph and tree used in the procedure to find a tie-set matrix. Let the branch voltages be V_b1, V_b2, V_b3, V_b4, V_b5, and V_b6 of respective branches. The tie-set matrix provides the fundamental KVL mesh equations as follows:

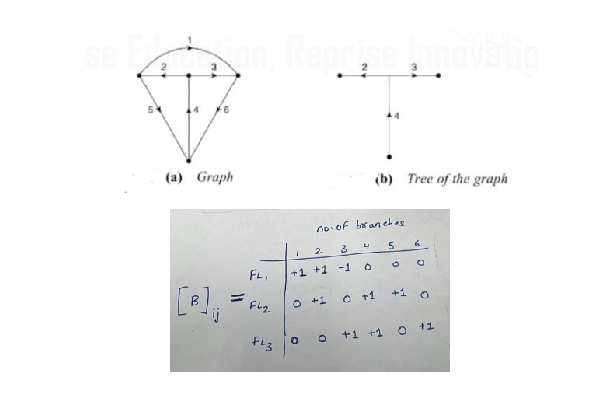
For fundamental loop 1, FL₁: V_b1 + V_b2 – V_b3 = 0

For fundamental loop 2, FL₂: V_b2+ V_b4+ V_b5 =0

For fundamental loop 3, FL₃: V_b3 + V_b4 + V_b6 =0

The above equations can be written in matrix form as,

[B]_ij [V_b]=0

Tie Set Matrix and KCL

Tie-set matrix is also used to write down the KCL equations. Consider the same graph and tree used for KVL equations as shown below. The branch currents I_b1, I_b2, I_b3, I_b4, I_b5, and I_b6 can be represented in terms of the fundamental loop currents i_L1, i_L2, and i_L3, as shown below:

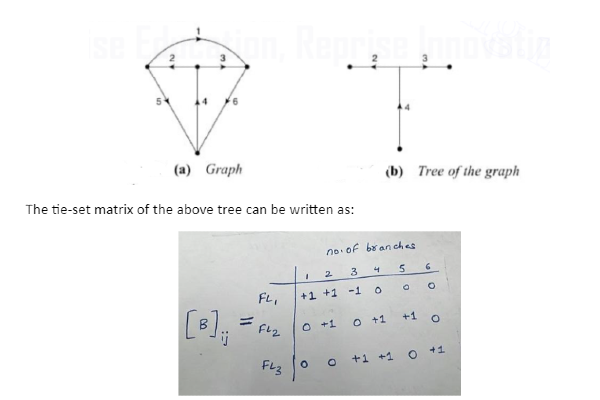
From the matrix column,

I_b1= i_L1

I_b2 = i_L1 + i_L2

I_b3 = – i_L1 + i_L3

I_b4 = i_L2 + i_L3

I_b5 = i_L2

I_b6 = i_L3

In matrix form, the above equation can be written as,

Important GATE Topics
And Gate Truth Table	Man Full Form
JK Flip Flop	Lan Full Form
JK Flip Flop Excitation Table	Propped Cantilever Beam
Job Sequencing With Deadlines	Torsional Force
Knapsack Problem Using Greedy Method	Pop Full Form