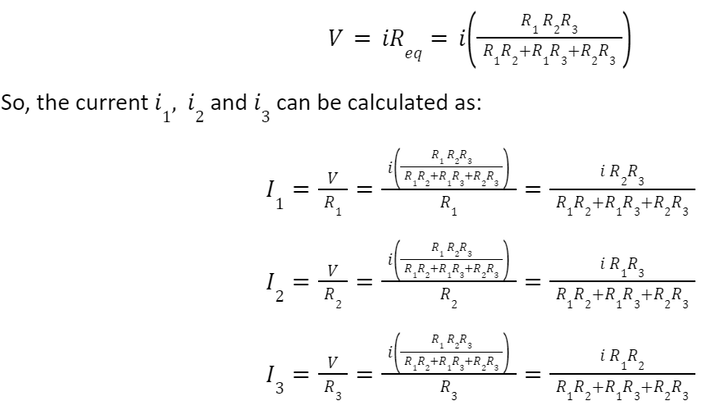- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Resistors in Parallel
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Resistors are connected in series or parallel in a complex network. An important circuit analysis technique involves replacing the resistors in parallel with an equivalent resistance in parallel for simplification. Resistors in parallel are basically current dividers circuits.
The voltage across the resistors in parallel is the same. Resistors in parallel have multiple paths for the current to flow. This article elaborates on the resistors in parallel and equivalent resistance of resistors in parallel, along with some examples.
Download Formulas for GATE Electronics & Communication Engineering – Control System
Table of content
Resistors in Parallel
When resistors are in parallel, the current gets divided between the resistors in parallel, and the voltage across all the resistors will be the same. If the resistors in parallel have the same resistance, then the current divides equally among all resistors. Resistors in parallel decrease the equivalent resistance of the circuit.
Resistors in parallel are treated as resistance current divider circuits. The power dissipated in the parallel circuit is much less, and maximum power is transmitted through these circuits.
Need for Parallel Combination of Resistors
In a parallel combination of resistors, the current gets divided between the resistors in parallel, and the voltage across all resistors is equal to the source voltage. A parallel combination can easily remove a resistor from the circuit without affecting the other resistors. Resistors are said to be in parallel combination when their two terminals are connected to the same two nodes, as shown below:
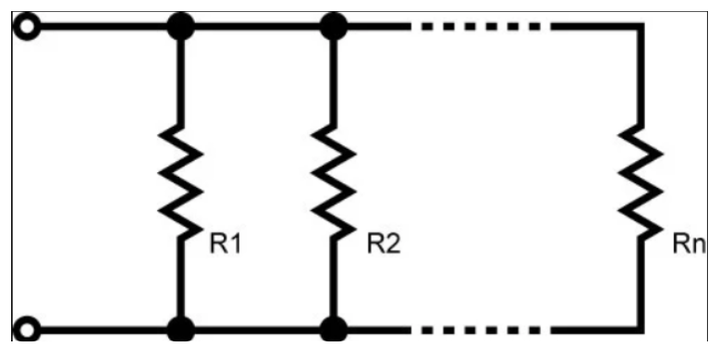
Resistors are connected in parallel for the following purposes:
- To decrease the overall resistance.
- To divide the source current between all the resistors.
- Resistors are connected in parallel combinations to deliver maximum power to the load.
Download Formulas for GATE Electronics & Communication Engineering – Digital Circuits
Equivalent Resistance of Resistors in Parallel
For simplification, let us calculate the equivalent resistance for the two resistors connected in parallel, as shown below:
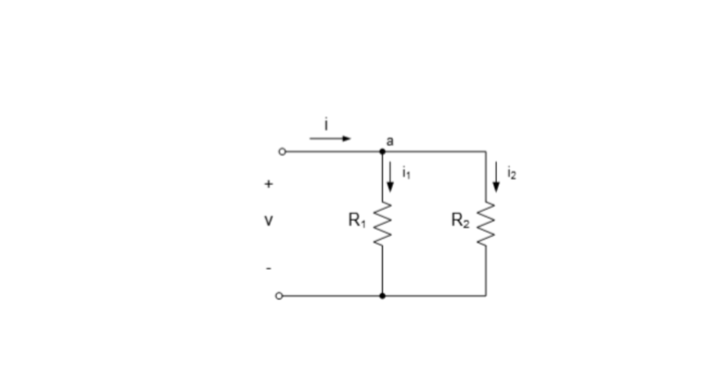
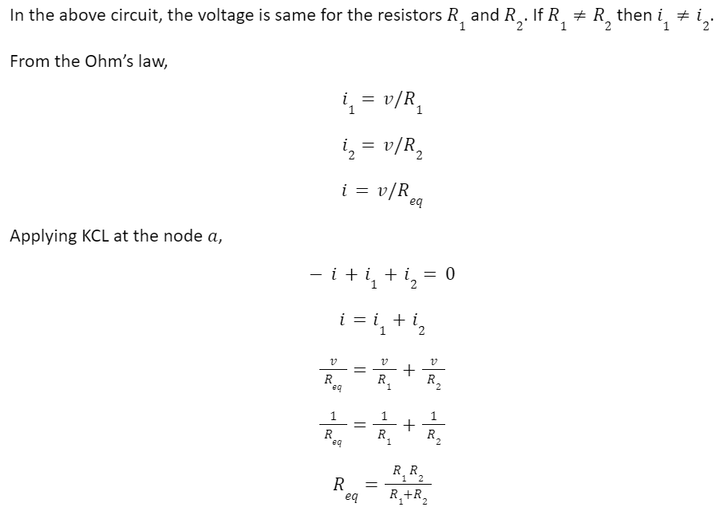

Where Req is the effective resistance of the circuit and can be modeled as:
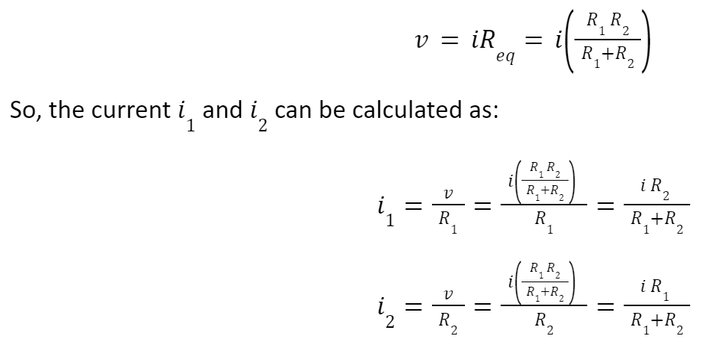
The source current i is divided between R1 and R2. This is known as the principle of current division.
Similarly, let us calculate the equivalent resistance for the three resistors connected in parallel, as shown below:
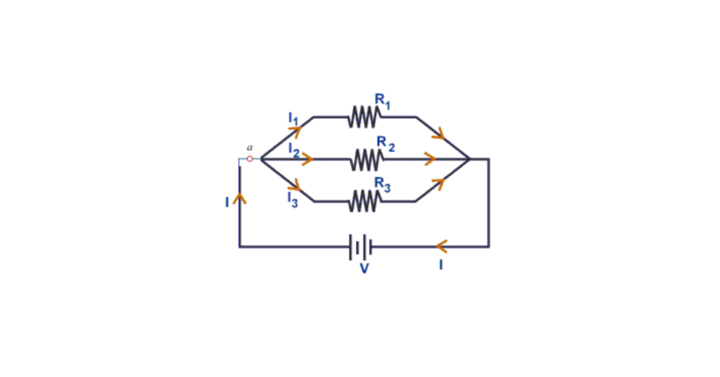

Where Req is the effective resistance of the circuit and can be modeled as:
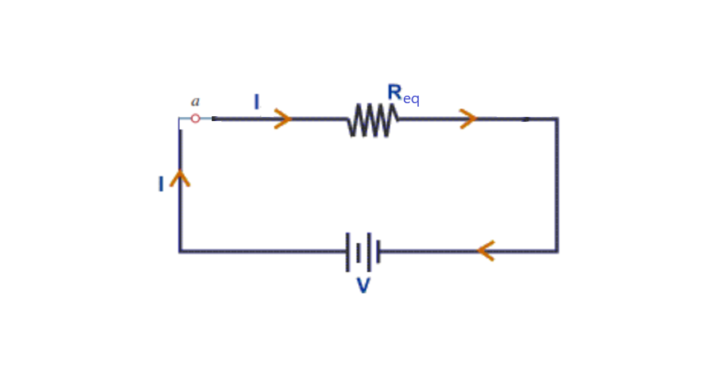
Download Formulas for GATE Electronics & Communication Engineering – Electronic Devices
Resistors in Parallel Formula
When N number of resistors are connected in parallel, then the overall equivalent resistance is given by:
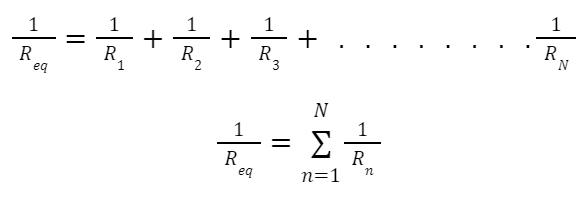
The equivalent resistance of resistors in parallel combination is always smaller than the resistance of the smallest resistor present in the circuit.
If there are N number of resistors connected in parallel and the values of all resistors are the same, i.e., R, then the overall resistance of the circuit is given by:
Req = R/N
In this case, the current also divides equally between all the resistors. If I am the total current and In is the current across the nth resistor, then:
In = I/N
Resistors in Parallel Examples
Example 1: Find the equivalent resistance seen from the terminal ab of the circuit shown below
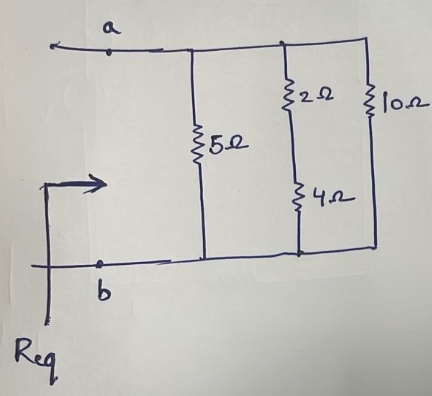
Solution: Resistance 2 Ω and 4 Ω are connected in series so that they will form an equivalent resistance of 6 Ω. The reduced circuitry be,
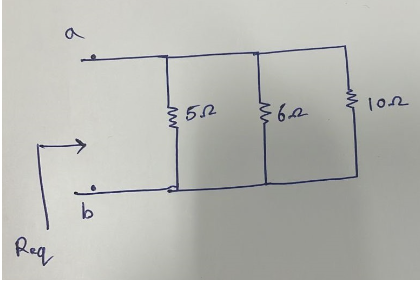
These resistors are in parallel, so
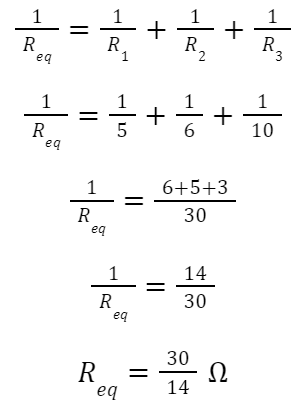
Example 2: Find the current i1 and i2 in the circuit shown below,
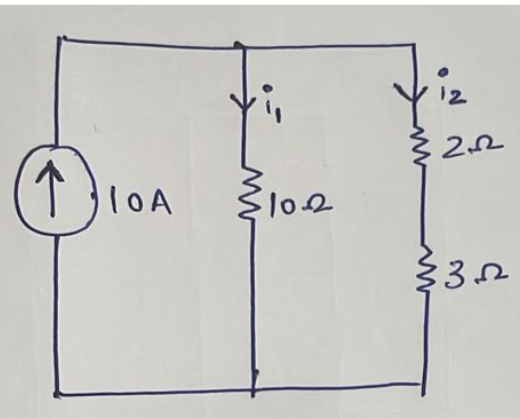
Solution: From the figure, resistance 2 Ω and 3 Ω are connected in series, so the circuit can be reduced as shown below,
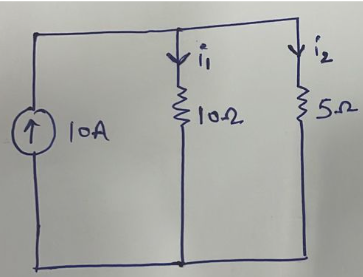
By using the current division rule,
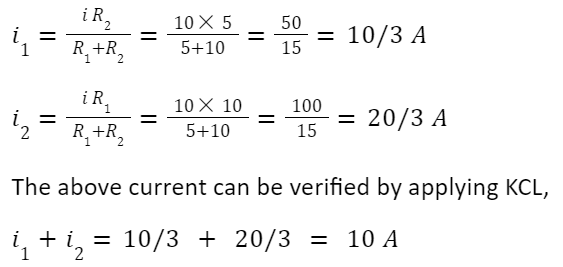
So, the answers are correct.