- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Millman’s Theorem
By BYJU'S Exam Prep
Updated on: September 25th, 2023

An electrical network theorem is a tool that is widely used to solve complex electrical problems. It was named after electrical engineering professor Jacob Millman who developed it. Millman’s Theorem is based on Thevenin’s and Norton’s theorem and is very effective in simplifying complex electrical circuits.
Millman’s Theorem, also known as the Parallel Generator theorem, is important for calculating voltage across the load and current through the load. There are two ways to use Millman’s theorem: it can be applied to circuits containing voltage sources alone or a mixture of voltage and current sources.
Table of content
What is Millman’s Theorem?
This method allows us to determine the voltage across parallel branches of the network. When several sources are connected, this method reduces the complexity of the network.
Millman’s Theorem Statement
A circuit with parallel voltage sources and internal resistance can replace one equivalent voltage source connected in series with an equivalent resistance.
We will look into it with a diagrammatic approach. The complex circuit arrangement in fig can be reduced to a simple network circuit.
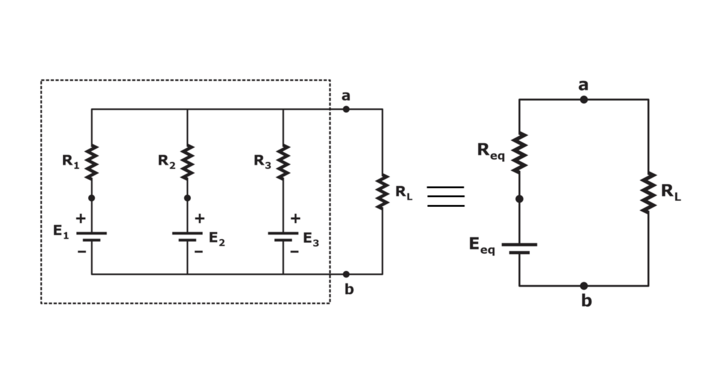

The negative sign is used because that supply has the opposite polarity of the other two.
Steps for Applying Millman’s Theorem
Following certain simple steps, we can summarize the application of the theorem to a valid electrical network. The steps are listed:
- Step 1:The circuit converts all voltage sources to current by dividing their potential by their internal resistance, Where G represents the conductance of the circuit.
I=E/R=EG
G=1/R
- Step 2: Calculate the circuit’s total current using the following mathematical expression.
Ieq=E1/R1+E2/R2+E3/R3+…+EN/RN
Ieq=(±E1G1)+(±E2G2)+(±E3G3)+…+(±ENGN)
- Step 3: The conductance of each current source can be calculated using mathematical expressions.
1/Req=1/R1+1/R2+1/R3+…+1/RN
Geq=G1+G2+G3+…+GN
- Step 4: Based on Ohm’s law, we can calculate the voltage at the open end of the parallel circuit.

- Step 5: Calculate the current flowing through the load circuit RL.
IL=Eeq/(Req+RL)
Advantages and Applications of Millman’s Theorem
Millman’s theorem can be used to simplify a complex network. Some common advantages and applications of the theorem are listed below.
- Millman’s Theorem changes voltage sources into current sources and vice versa in circuits with voltage and current sources.
- Millman’s theorem can be applied to determine the voltage across a set of parallel branches when sufficient voltage sources are present to prevent a solution based on the series-parallel reduction method.
- Millman’s Theorem is elementary to utilize because it doesn’t need the utilization of instantaneous equations. Typical applications include circuits whose topology is complex, using many Op-amps.
Limitations of Millman’s Theorem
Despite the generic nature of Millman’s theorem, the application of the theorem is restrained by some conditions, and it does not apply to every circuit. The conditions which need to be satisfied for the application of the theorem are:
- Millman’s Theorem does not cover circuits with impedances among independent sources.
- Millman’s Theorem does not apply to circuits where dependent sources complement independent sources.
- There is no application of this theorem when two independent sources exist in the circuit.
Millman’s Theorem Example
Using Millman’s theorem, find the current through and the voltage across the load resistor; RL is shown in the figure.
Solution:
Now, the current through and the voltage across RL is (E represents the potential)
Step 1: Converting voltage source to current source by dividing with their respective resistance
I1=E1/R1=-20/2=-10
I2=E2/R2=10/3=3.334
I3=E3/R3=8/4=2
Step 2: Calculating the equivalent current
Ieq=-20/2+10/3+8/4=-56/12
Step 3: Calculating the equivalent resistance
1/Req=1/R1+1/R2+1/R3
Req=12/13
Step 4: Calculating the equivalent potential
Eeq=Ieq.Req=-56/13
Step 5: Calculating current through RL
IL=Eeq/(Req+RL)=-0.727
From Ohm’s law
VL= (–0.727) × 5 = –3.635 volts


