Cardinality in DBMS
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Before jumping onto Cardinality in DBMS, let us first discuss the mapping cardinality or cardinality ratio. In the “Cardinality in DBMS,” the cardinality ratio tells the number of entities to which another entity can be associated via a relationship set. Mapping cardinality or cardinality ratio uses the binary relationship set in the Cardinality in DBMS.
In a database management system, “cardinality” refers to the maximum number of relationship instances in which an entity can participate. In this article, we will learn about cardinality in DBMS and its various relations.
Download Formulas for GATE Computer Science Engineering – Programming & Data Structures
Table of content
What is Cardinality in DBMS?
The cardinality in DBMS is most useful in describing binary relation sets, but it can also help to describe relation sets with more than two entity sets. Cardinality in databases describes the connections between the data in two database tables.
Define Cardinality in DBMS
The cardinality in DBMS refers to the number of entities to which another entity can be linked via a given relation set. It shows the number of times instances of one thing are connected to another.
Let us see the various cardinalities that exist in DBMS. We will only consider binary relation sets here, which means we will look for the relationship between entity sets E1 and E2 for the set R.
Download Formulas for GATE Computer Science Engineering – Discrete Mathematics
Types of Cardinality in DBMS
4 different relations exist in DBMS. The cardinality in DBMS that is possible for binary relationships is as follows:
- One to One(1: 1)
- One to Many(1: M)
- Many to One(M: 1)
- Many to Many(M: M)
One to One(1: 1)
A one-to-one relationship exists when only one instance of an individual is connected with, at most, one entity of another (same) entity set via relationship instance. An entity(tuple) in E1 is associated with at most one entity(tuple) in E2, and an entity in E2 is associated with at most one entity in A.
For example, in the following ER diagram, entity E1 and entity E2 have one-to-one mapping on the relation R. The candidate key for the entity set E1 is A, and for the entity set E2, B is the candidate key.
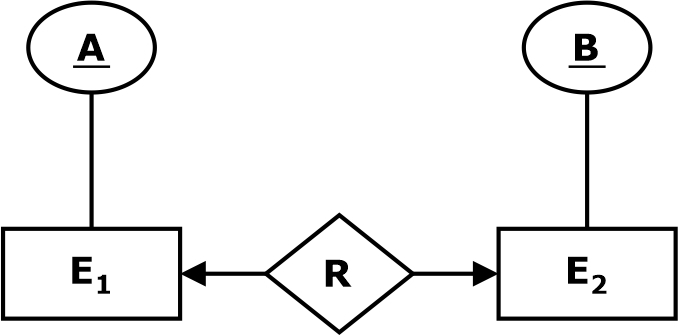
The candidate keys of relation R(A, B) = A, B
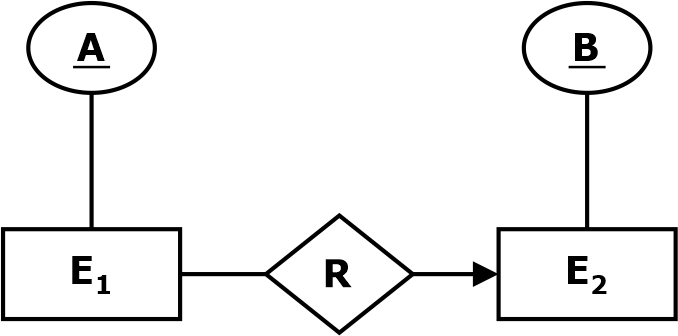
One to Many (1: M)
A one-to-many relationship exists when only one instance of an entity is connected with many entities of another entity set via relationship instances. An entity(tuple) in E1 is associated with zero or more entities in E2, but an entity in E2 can be associated with at most one entity in E1.
For example, in the following ER diagram, entity E1 and entity E2 have the one-to-many mapping on the relation R. The candidate key for the entity set E1 is A, and for the entity set E2, B is the candidate key.
Candidate key of R (A, B) = B
Download Formulas for GATE Computer Science Engineering – Algorithms
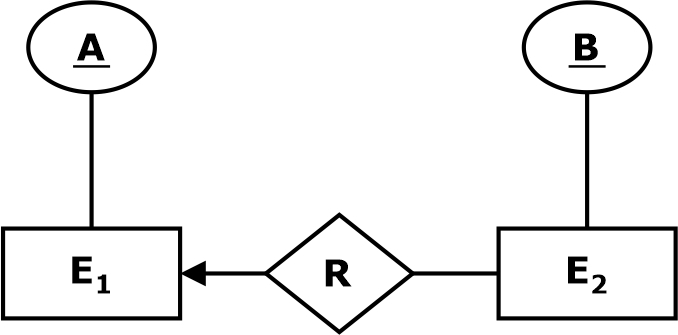
Many to One (M: 1)
A many-to-one relationship exists when more than one instance of the entity set is on the left, and only one instance of the entity set on the right is associated with the relationship. An entity(tuple) in Ę2 is associated with zero or more entities in E1 but an entity in
E1 can be associated with at most one entity in E2.
For example, in the following ER diagram, the entities E1 and E2 have the many-to-one mapping on the relation R. The candidate key for the entity set E1 is A, and for the entity set E2, B is the candidate key.
Candidate key of R (A, B) = A
Many to Many (M: M)
A many-to-many relationship exists when more than one instance of the entity set is on the left and more than one entity of another entity set is on the right associated with the relationship. An entity(tuple) in E2 is associated with zero or more entities in E1, and an entity(tuple) in E1 is associated with zero or more entities in E2.
For example, in the following ER diagram, entity E1 and entity E2 have many-to-many mapping on the relation R. The candidate key for the entity set E1 is A, and for the entity set E2, B is the candidate key.
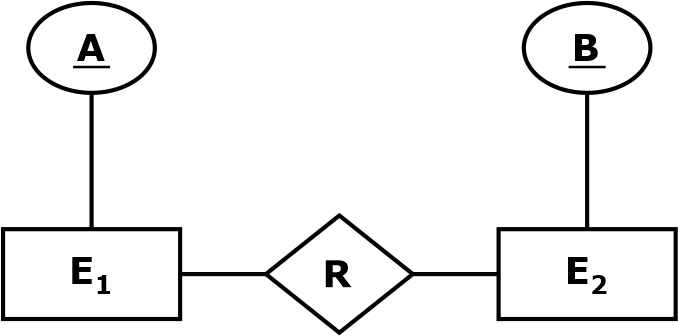
Candidate key of R(A, B) = AB


