- Home/
- GATE ELECTRICAL/
- GATE EE/
- Article
Basic Signal Operation
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Analyzing signals and systems certainly demands some basic signal operations. For the continuous-time signals, time and amplitude are two variables. Hence there may be a need to perform certain basic signal operations like amplitude-scaling, addition, subtraction, and multiplication with amplitude; and concerning time, the operations like time-scaling, time-shifting, and time-reversal.
Understanding certain basic signal operations can help make signals easier to understand and use in various situations. Check the operations on suitable signals below to better understand these basic signal operations.
Download Formulas for GATE Electronics & Communication Engineering – Control System
Table of content
What is the Basic Signal Operation?
Signals can be subjected to several processes to produce new signals. Here, we have provided in-depth details about the following.
- Basic signal operations on Amplitude
- Basic signal operations on Time
Basic Signal Operations on Amplitude
Concerning amplitude, we can perform four basic signal operations, namely-
- Amplitude Scaling
- Addition
- Subtraction
- Multiplication
Download Formulas for GATE Electronics & Communication Engineering – Digital Circuits
Amplitude Scaling Signal Operation
The Amplitude scaling operation is applied to a continuous-time signal to increase or decrease its amplitude. If x(t) is any continuous-time signal, then.
Ax(t) is the amplitude scaling version of the signal x(t), where A is always a positive value.
If |A|>1→ Increase the amplitude of the signal
If |A|<1→ Decrease the amplitude of the signal
We can understand it better with the following example.
A = 1
|A|>1
|A|<1
Download Formulas for GATE Electronics & Communication Engineering – Electronic Devices
Addition Signal Operation
If we add two continuous-time signals, x(t) and y(t), the resultant signal will have an amplitude equal to the sum of their amplitudes. The below example can be used to explain it in a better way.
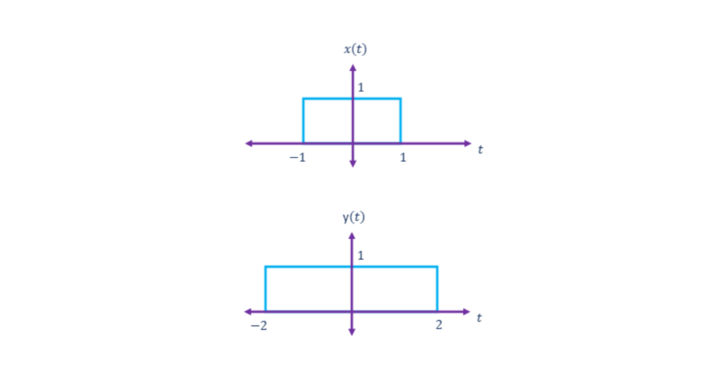
From the above figures, the amplitude of the signal
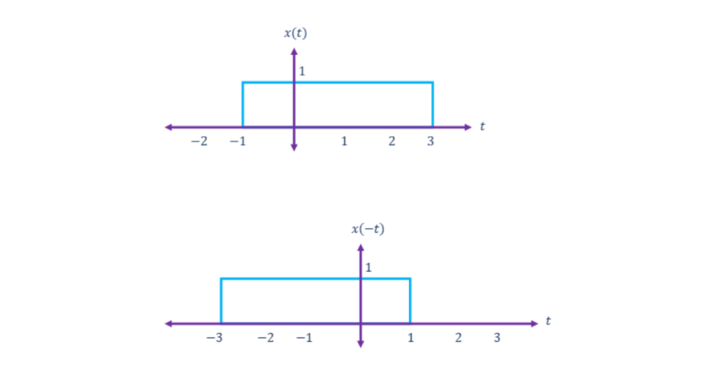
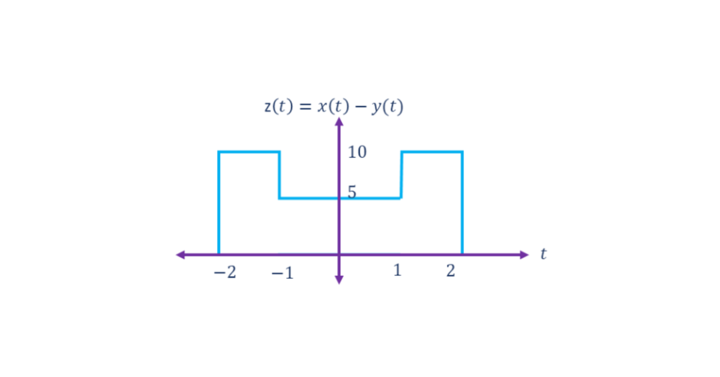
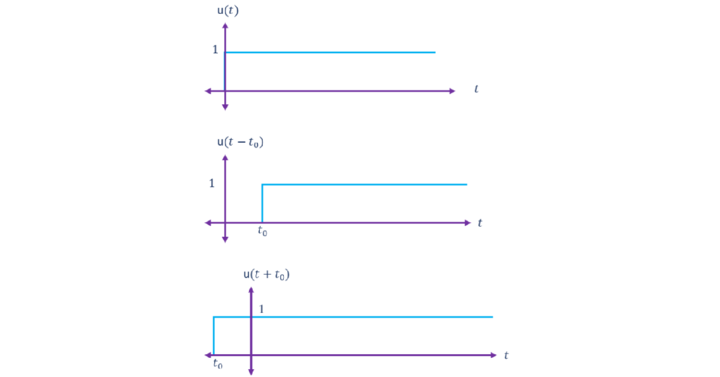
z(t)=x(t)+y(t) between the interval -2 z(t)=x(t)+y(t)=0+1=1 The amplitude of the signal z(t) between the interval −1 z(t)=x(t)+y(t)=1+1=2 The amplitude of the signal z(t) between the interval 1 The subtraction operation of two signals is similar to that of addition, as the amplitude of the resultant signal is the value obtained from the subtraction of the amplitudes of the two individual signals in their respective intervals. Follow the below example to understand this better. If z(t) is the signal that is obtained from subtracting y(t) from x(t) then the value of the amplitude of the signal z(t) in the interval −2 z(t)=x(t)−y(t)=10−0=10 The Amplitude of the signal z(t) in the interval −1 z(t)=x(t)−y(t)=10−5=5 The Amplitude of the signal z(t) in the interval 1 z(t)=x(t)−y(t)=10−0=10 Just like addition and subtraction, the multiplication of two signals is the multiplication of the amplitudes of the two signals at their respective intervals. We can understand it better with the following example. −2 z(t)=x(t)×y(t)=2×0=0 The Amplitude of the signal z(t) in the interval −1 z(t)=x(t)×y(t)=2×1=2 The Amplitude of the signal z(t) in the interval 1 isz(t)=x(t)×y(t)=2×0=0 Concerning time, the following signal operations can be done. The time-scaling operation on the continuous-time signal is to expand or compress the signal on its time axis. If a continuous-time signal x(t) is scaled with a factor ‘a’ then x(at)x(at) will represent its time-scaled version; here, ‘a’ is any positive value. If |a|>1→a>1→Expansion of the signal If |a|<1→a<1→Compression of the signal. The below example will help us understand this concept better. The time-shifting of the continuous-time signal is shifting the signal to its left to make an advance or shifting to its right to induce some delay to the signal. If x(t) is a continuous-time signal, then x(t±t0) is the time-shifted version of x(t). x(t+t0) → Advanced version (or) a Negative shift (or) Left shift x(t−t0) → Delayed version (or) a Positive shift (or) Right shift We can view the following example better by considering a unit step signal u(t). If we want the mirror-image of the signal across the vertical axis or to rotate vertically by an angle of 180º, then we operate time-reversal. If x(t) is a continuous-time signal, then x(-t) is its time-reversal version. Follow the below example for a better understanding.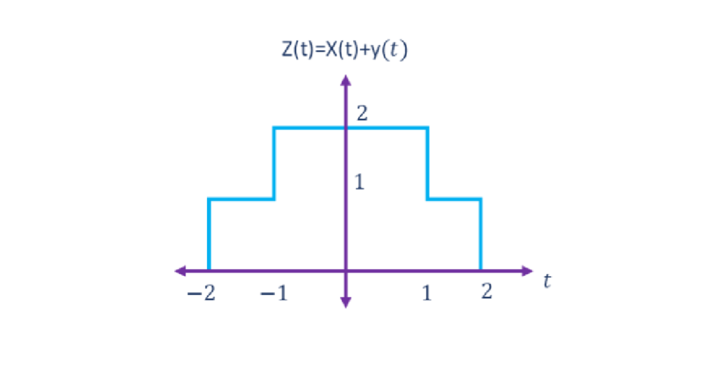
Subtraction Signal Operation
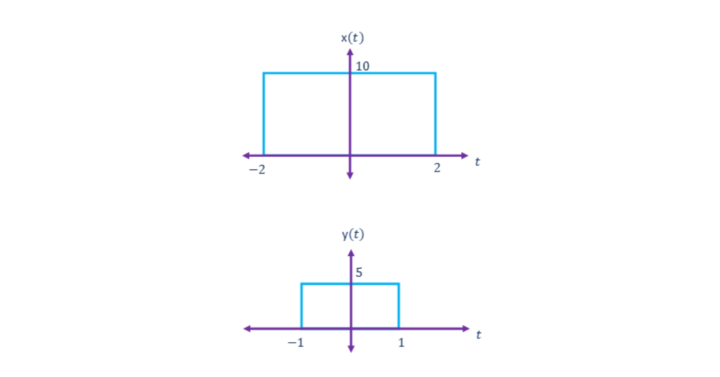
Multiplication Signal Operation
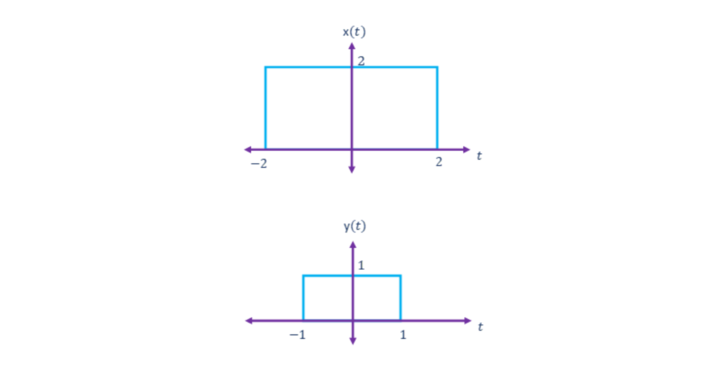
If z(t) is the signal that is obtained from multiplying the signals x(t) and y(t) then, the value of the amplitude of the signal z(t) in the interval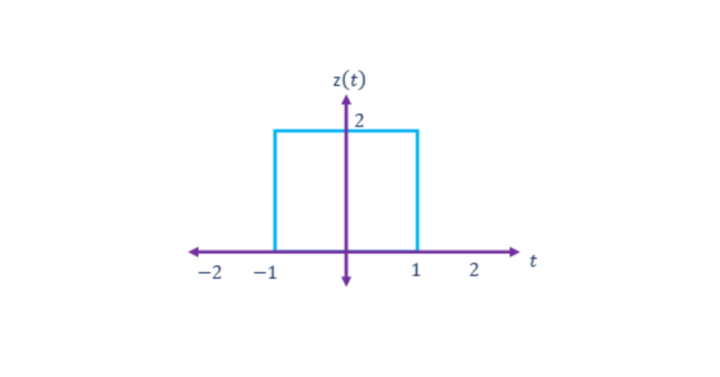
Basic Signal Operations on Time
Time-Scaling of Signals
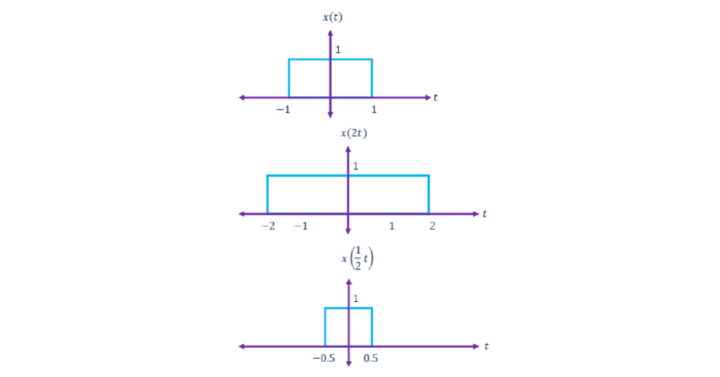
Time-Shifting of Signals
Time-Reversal of Signals