Crop Water Requirement
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Water Requirement of Crops is one of the important topics of the GATE and other competitive exams asked in the Irrigation engineering subject. In the topic of the water requirement of crops, water required for the growth of crops is calculated, and different water limit at which crop can survive is studied.
Water Requirement of Crops PDF
The topic water requirement of crops consists of the many parameters which govern the overall growth of crops. The article contains fundamental notes on the “Water Requirement of Crops” topic of the “Irrigation Engineering” subject.
Table of content
-
1.
What is Meant by the Water Requirement of Crops?
-
2.
Different Terms Related to Crop Water Requirements
-
3.
Layout of the Canal System
-
4.
Importance of Duty
-
5.
Factors Affecting the Duty of Water
-
6.
Types of Irrigation Efficiencies
-
7.
Concept of Consumptive Irrigation Requirement (CIR)
-
8.
Water Requirements of Crops Questions
What is Meant by the Water Requirement of Crops?
The water requirement of crops is the quantity required for a particular crop’s growth. Every crop requires a certain quantity of water after a certain fixed interval throughout its period of growth. If natural rain is sufficient and timely to satisfy these requirements, no irrigation water is required to raise that crop.
In a tropical country like India, the natural rainfall is either insufficient or rare. In such cases, certain crops require various irrigation techniques in a certain part of the country. The area where irrigation is a must for agriculture is called the arid region, while the area where inferior crops can be grown without irrigation is called a semiarid region.
Different Terms Related to Crop Water Requirements
Water requirements of crops are the topic in which the water requirement for the proper growth of crops is calculated. Crop water requirement is an essential chapter for the GATE CE exam. These requirements are calculated based on the different parameters which are described below.
Crop Period or Base Period
The time period that elapses from the instant of its sowing to the instant of its harvesting is called the crop period.
The time between the first watering of a crop at the time of its sowing to its last watering before harvesting is called the base period or the base of the crop.
Crop period is slightly more than the base period, but for all practical purposes, they are taken as one and the same thing and generally expressed in days.
Delta of a Crop (Δ)
Each crop requires a certain amount of water after a certain fixed interval of time throughout its period of growth.
The total quantity of water required by the crop for its full growth might be expressed in hectare meter (ha.m) or simply as the depth to which water would stand on the irrigated area if the total quantity supplied were to stand above the surface without percolation or evaporation. This total depth of water (in cm) required by a crop to come to maturity is called its delta (Δ).
Delta for Crops
The average values of deltas for certain crops are shown in the table. These values represent the total water requirement of the crops. The actual requirement of irrigation water may be less, depending upon the useful rainfall. Moreover, these values represent the values on the field, i.e. ‘delta on field’, which includes losses.
| Average Approximate Values of Δ for Certain Important Crops in India | |
| Crop | Delta on field(cm) |
| Sugarcane | 120 |
| Rice | 120 |
| Tobacco | 75 |
| Garden fruits | 60 |
| Cotton | 50 |
| Vegetables | 45 |
| Wheat | 40 |
| Barley | 30 |
| Maize | 25 |
| Fodder | 22.5 |
Duty of Water (D)
The term duty means the area of land that can be irrigated with the unit volume of irrigation water. Quantitatively, duty is defined as the area of land expressed in hectares that can be irrigated with unit discharge, 1 cumec flowing throughout the base period, expressed in days.
If water flowing at a rate of one cubic meter per second runs continuously for B-days and matures 200 hectares, then the water duty for that particular crop will be defined as 200 hectares per cumec to the base of B days. Hence, duty is the area irrigated per cumec of discharge running for base period B. The duty is generally represented by the letter D.
Relation between Duty(D) and Delta(Δ)
Let there be a crop of base period B days. Let one cumec of water be applied to this crop on the field for B days. Now, the volume of water applied to this crop during B days.
Volume of water applied to crop = V = (1 x60 x60 x24 xB) m3. = 86400 B (cubic meter)
By duty (D) definition, one cubic meter supplied for B days matures D hectares of land.
This quantity of water (V) matures D hectares of land or 104 D sq.m of area.
Total depth of water applied on this land = Volume/ Area = 86,400 B/ 104 D . 8.64B/D metres
By definition, this total depth of water is called delta (Δ).
So, Δ = 8.64 B/D (metres)
Where
- Δ is in meters, B is in days; and
- D is duty in hectares/cumec.
Layout of the Canal System
The duty of water for a crop is the number of hectares of land the water can irrigate. Therefore, fewer hectares of land will irrigate if the crop’s water requirement is higher. Hence, if water consumed is more, duty will be less. Therefore, it becomes clear that the water duty at the head of the watercourse will be less than that because when water flows from the watercourse and reaches the field, some water is lost as transit losses.
During the passage of water from these irrigation channels, water is lost due to evaporation and percolation. These losses are called Transit losses or Transmission or Conveyance losses in channels.
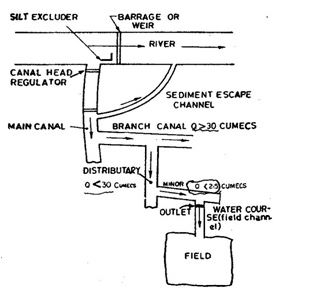
Applying the same reasoning, it can be established that the duty of water at the head of a minor will be less than that at the head of the watercourse; duty at the head of a distributary will be less than that at the head of a minor, duty at the head of a branch canal will be less than that at the head of a minor, duty at the head of the main canal will be less than the duty at the head of a branch canal.
Importance of Duty
Duty helps us in designing an efficient canal irrigation system. Knowing the total available water at the head of the main canal and the overall duty for all the crops required to be irrigated in different seasons of the year, the area which can be irrigated can be worked out. Inversely, if we know the corps area required to be irrigated and their duties, we can work out the discharge required for designing the channel.
Duty of water, therefore, varies from one place to another and increases as we move downstream from the head of the main canal towards the head of the branches or watercourses. The duty at the head of the watercourse (i.e. at the outlet point is generally the endpoint of the Irrigation Department.
Factors Affecting the Duty of Water
The duty of water is dependent upon several factors. Some of the important factors through which the duty of water is affected are given below.
- Climatic and season: As stated earlier, duty includes the water lost in evaporation and percolation. These losses will vary with the season. Hence, duty varies from season to season and also from time to time in the same season. The figures for duties we generally express are average values considered over the entire crop period.
- Useful rainfall: If some of the rain, falling directly over the irrigated land, is useful for the growth of the crop, then so much less irrigation water will be required to mature the crop. The more useful rainfall less will be the requirement of irrigation water, and hence more will be the duty of irrigation water.
- Type of soil: If the permeability of the soil under the irrigated crop is high, the water lost due to percolation will be more, and hence, the duty will be less. Therefore, the duty of water is less for sandy soils, where the permeability is more.
- Efficiency of the cultivation method: If the cultivation method (including tillage and irrigation) is faulty and less efficient, resulting in the wastage of water, the duty of water will naturally be less. If the irrigation water is used economically, then the duty of water will improve, as the same quantity of water would be able to irrigate more area. Cultivators should, therefore, be trained and educated properly to use irrigation water economically.
Types of Irrigation Efficiencies
Efficiency is the ratio of the water output to the water input and is usually expressed as a percentage. Input minus output is nothing but losses; hence, if losses are more, the output is less, and efficiency is less. Hence, efficiency is inversely proportional to the losses. Water is lost in irrigation during various processes; therefore, there are different kinds of irrigation efficiencies, as given below.
(i) Efficiency of water-conveyance (ηc): It is the ratio of the water delivered into the fields from the outlet point of the channel to the water pumped into the channel at the starting point. It may be represented by ηc. It takes the conveyance or transit losses into account.
(ii) Efficiency of water application (ηa): It is the ratio of the quantity of water stored in the root zone of the crops to the quantity of water delivered into the field. It may be represented by ηa. It may also be termed farm efficiency, as it considers the water lost on the farm.
(iii) Efficiency of water storage (ηs): It is the ratio of the water stored in the root zone during irrigation to the water needed in the root zone before irrigation (i.e., field capacity –existing moisture content). It may be represented by ηs.
(iv) Efficiency of water use (ηu): It is the ratio of the water beneficially used, including leaching water, to the quantity of water delivered. It may be represented by ηu.
(v) Uniformity coefficient or Water distribution efficiency
The effectiveness of irrigation may also be measured by its water distribution efficiency (ηd), which is defined below:
ηd = (1-d/D)x100
Where
- ηd = Water distribution efficiency
- D = Mean depth of water stored during irrigation.
- d = Average of the absolute values of deviations from the mean.
The water distribution efficiency represents the extent to which the water has penetrated to a uniform depth throughout the field. When the water has penetrated uniformly throughout the field, the deviation from the mean depth is zero, and the water distribution efficiency is 1.0.
(vi) Consumptive Use or Evapotranspiration (Cu)
Consumptive use for a particular crop may be defined as the total amount of water used by the plant in transpiration (building of plant tissues, etc.) and evaporation from adjacent soils or plant leaves at any specified time. The values of consumptive use (Cu) may differ for different crops and for the same crop at different times and places.
In fact, the consumptive use for a given crop at a given place may vary throughout the day, the month, and the crop period. Values of daily or monthly consumptive use are generally determined for a given crop and at a given place. Values of monthly consumptive use over the entire crop period are then used to determine the irrigation requirement of the crop.
Concept of Consumptive Irrigation Requirement (CIR)
It is the amount of Irrigation water required to meet the evapotranspiration needs of the crop during its full growth. Therefore, it is nothing but the consumptive use itself, exclusive of effective precipitation, stored soil moisture, or groundwater. When the last two are ignored, then we can write
CIR = Cu – Re
Effective Rainfall (Re)
Precipitation falling during the growing period of a crop that is available to meet the evapotranspiration needs of the crop is called effective rainfall. It does not include precipitation lost through deep percolation below the root zone or the water lost as surface runoff.
Net Irrigation Requirement (NIR)
It is the amount of irrigation water required in order to meet the evapotranspiration need of the crop as well as other needs such as leaching. Therefore, N.I.R. = Cu –Re + Water lost as percolation in satisfying other needs such as leaching.
Consumptive use or evapotranspiration depends upon all those factors on which evaporation and transpiration depend, such as temperature, sunlight, humidity, wind movement, etc.
Estimation of Consumptive Use
Although various methods have been developed in order to estimate the evapotranspiration (consumptive use) value of a crop in an area, the most simple and commonly used methods are:
(1) Blaney–Criddle Equation, and
(2) Hargreaves class a pan evaporation method
Blaney-Criddle Formula
It states that the monthly consumptive use is given by
Cu = (K.P/ 40) [1.8t + 32]
where
- Cu = Monthly consumptive use in cm.
- k = Crop factor, determined by experiments for each crop under the environmental conditions of the particular area.
- t = Mean monthly temperature in oC
- p = Monthly pet cent of annual daylight hours that occur during the period.
If p/40 [1.8t +32] is represented by f, we get
Cu = k.f
Water Requirements of Crops Questions
Solving an example of this topic strengthens the concept related to that. Here such an example is shown that enhances the related concept of consumptive use of the crops.
Example 1: The monthly consumptive use values for Paddy are tabulated in Table. Determine the total consumptive use. What is the average monthly consumptive use and peak monthly consumptive use?
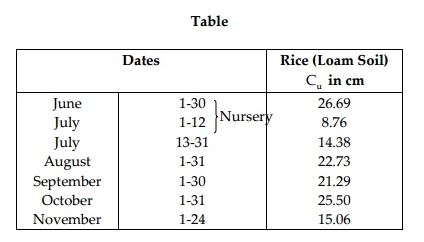
Solution: The summation of consumptive uses
= 29.69+8.76+14.38+22.73+21.29+25.50+15.06 = 137.41 cm
Hence, total consumptive use for paddy = 137.41 cm.
Average daily consumptive use = 137.4/Period of growth in days
= 137.41/31+31+31+30+31+24
= 137.41/177 = 0.77 cm. = 0.77×30=23.1 mm
Average monthly consumptive use = 0.77 × 30 = 23.1 mm.Peak monthly consumptive use = 26.69 cm. (Highest value is given)
Example 2: If rice requires about 10cm depth of water at an average interval of about 10 days, and the crop period for rice is 120 days, find out the delta for rice.
Solution: Water is required at an interval of 10 days for a period of 120 days. It means that 12 no. of waterings are required, and each time, 10 cm depth of water is required. Therefore, the total depth of water is required.
= 12 x10 cm = 120 cm.
Hence Δ for rice = 120 cm.
Example 3: If wheat requires about 7.5 cm of water after every 28 days, and the base period for wheat is 140 days, find out the value of the delta for wheat.
Solution: Assuming the base period represents the crop period, as per usual practise, we can easily infer that the water is required at an average interval of 28 days up to a total period of 140 days.
This means that 5(140/28) no. of waterings are required 28 days
The depth of water required each time = 7.5 cm.
The total depth of water required. In 140 days = 5 x7.5 = 37.5 cm
Hence, Δ for wheat = 37.5 cm.
Example 4: Once a cumec of water is pumped into a farm distribution system. 0.8 cumec is delivered to a turnout 0.9 kilometers from the well. Compute the conveyance efficiency.
Solution: By definition
ηc = Output/ Input x 100 = 0.8/1.0 . 100 = 80%
Example 5: 10 cumecs of water are delivered to a 32-hectare field for 4 hours. Soil probing indicated that 0.3 metres of water has been stored in the root zone. Compute the water application efficiency.
Solution: Volume of water supplied by 10 cumecs of water applied for 4 hours =(10 x 4 x 60x 60)m3 = 1,44,000 m3
= 14.4 x104 m3 = 14.4m x 104m2 = 14. 4ha.m.
Depth of water applied =
volume/area = 1,44, 000/32,0,000 = 144/320 = 0.45
Input = 14.4 ha.m
Output = 32 hectares of land storing water upto 0.3 m depth,
Output = 32×0.3 ha.m = 9.6 ha.m
Water application efficiency (ηa) = Output/ Input x 100 =( 9.6/14.4) x 100= 67%
Example 6: A stream of 130 litres per second was diverted from a canal, and 100 litres per second were delivered to the field. An area of 1.6 hectares was irrigated in 8 hours. The effective depth of the root zone was 1.7 m. The runoff loss in the field was 420 cubic meter. The depth of water penetration varied linearly from 1.7 m at the head end of the field to 1.1 m at the tail end. The available moisture-holding capacity of the soil is 20 cm per metre depth of soil. It is required to determine the water conveyance efficiency, water application efficiency, water storage efficiency, and water distribution efficiency. Irrigation was started at a moisture extraction level of 50% of the available moisture.
Solution:
(i) Water conveyance efficiency (ηc) = ( Water delivered to the fields/ Water supplied into the canal at the head) x 100
= 100/130 x 100 =77%
(ii) Water application efficiency (ηa)
Water stored in the root zone during irrigation / Water delivered to the field x 100
Water was supplied to the field for 8 hours @ 100 liters per second
= 100x8x60x60 litres = 2880 cubic meter
Runoff loss in the field = 420 cubic meter
the water stored in the root zone = 2880 –420 = 2460 cubic meter
(iii) Water application efficiency (ηa)
= 2460 /100 = 85.4% Ans. 2880
(iv) Water storage efficiency (ηs) = (Water stored in the root zone during irrigation /
Water needed in the root zone before irrigation) x 100
Moisture holding capacity of soil
= 20 cm per m depth x1.7 m depth of root zone = 34 cm
Moisture already available in the root zone at the time of the start of irrigation
= 50/100 x 34 =17cm.
Additional water is required in the root zone
= 34 –17 = 17 cm.
= 2720 cubic meter
But actual water stored in the root zone = 2460 cubic meter
Water storage efficiency (ηs) =2460 /2720 x 100 90% (say)
(v) Water distribution efficiency
Where D = mean depth of water stored in the root zone
D = ( 1.7+1.1 )/2 = 1.4m
d is computed as below:
Deviation from the mean at the upper end (absolute value) = |1.7 -1.4| = 0.3
Deviation from the mean at lower end = | 1.1 -1.4 | =0.3
d = Average of the absolute values of deviations from mean = 0.4 +0.3/2 = 0.35
Using equations, we have,
ηd = 75 or 75%
If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE:
Online Classroom Program for ESE/GATE CE
You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams:



