What is Volumetric Strain? Definition & Formula

What is Volumetric Strain?

Volumetric strain is defined as the ratio of change in the volume of a body to its original volume due to the application of some external deformation-causing forces. It is also known as Dilation and is important for the GATE exam. The general equation for volumetric strain is given as -

E_V = ΔV/V

where

• ΔV = change in volume
• V = original volume

Bulk Modulus (K): When a body is subjected to stresses of equal intensity in 3 mutually perpendicular directions, then the ratio of this direct stress to the volumetric strain is called Bulk modulus. It is generally denoted by K.

K =Direct Stress/Volumetric strain= σ/E_V

_{Download Formulas for GATE Civil Engineering - Irrigation & Hydrology}

Volumetric Strain for Rectangular Bar

This section will derive the volumetric strain formula for a rectangular bar. To define volumetric strain expression for a rectangular bar, let us assume a rectangular prismatic member of length L, width B, and depth D subjected to triaxial stresses, as shown in the figure below.

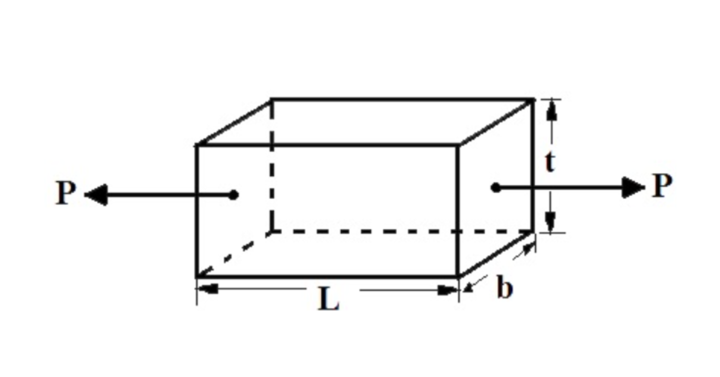
The initial volume of the rectangular bar,

V = L×B×D

The change in volume due to the applied stresses,

ΔV = δL×B×D + L×δB×D + L×B×δD

We know that volumetric strain,

E_V=ΔV/V

E_V=δL/L+δB/B+δD/D

We know that,

δL/L = E_x (strain in the x-direction)

δB/B = E_y (strain in the y-direction)

and δD/D = E_z (strain in the z-direction)

So,

E_V = E_x+E_y+E_z....(i)

We also know that,

E_x = σ_x/E-μσ_y/E-μσ_z/E

E_y = σ_y/E-μσ_x/E-μσ_z/Eand

E_z = σ_z/E-μσ_x/E-μσ_z/E

where

• μ = Poisson's ratio
• E = Young’s modulus of elasticity

Putting the value of x, y and z in equation (i)

E_V=σ_x/E-μσ_y/E-μσ_z/E +σ_y/E-μσ_x/E-μσ_z/E +σ_z/E-μσ_x/E-μσ_z/E

E_V= (1-2μ) (σ_x+σ_y+σ_z)/E

Formulas for GATE Civil Engineering - Fluid Mechanics

Volumetric Strain for Cylindrical Rod

In this section, we will derive the volumetric strain formula for a cylindrical rod. To define volumetric strain expression for a cylindrical rod, let us assume a cylindrical rod of length L and diameter d as shown in the figure below

The initial volume of the cylindrical rod,

V=(π/4)d².L

The change in volume due to applied stresses

ΔV=(π/4)[d².δL+L.2dδd]

We know that volumetric strain,

E_V=ΔV/V

E_V=[δL/L+2. δd/d]

We know that,

δL/L=E_L (strain in the longitudinal direction)

δd/d=E_d (strain in the radial direction)

So,

E_V=E_L+2E_d

Volumetric Strain for a Spherical Body

In this section, we will derive the volumetric strain formula for a spherical body. To define volumetric strain expression for a spherical body, let us assume a sphere of diameter d, as shown in the figure below.

The initial volume of the sphere,

V=(π/6)d³

The change in volume due to applied stresses

V=(π/6).3δd.d²

We know that volumetric strain,

E_V=ΔV/V

E_V=3δd/d

E_V=3E_d