Principal Stress
By BYJU'S Exam Prep
Updated on: September 25th, 2023

We can define principal stress as when any load is applied to a body, normal and shear stresses are developed. Due to this, applied loading concentrated on a point where all three planes X, Y, and Z, are perpendicular to that point. The resultant stress on these planes is called principal stress.
The sustainability of principal stress is to check the allowable maximum force on a body, and this force is designed according to the normal stress. All normal stress centred at a location on a plane is defined as resultant principal stress. For any structural design, we always consider the design stress. Hence to design the structure, we need to know the maximum or minimum stress this is the sustainability of principal stresses.
Table of content
What is Principal Stress?
Principal stress is the maximum or minimum normal stress which may be developed on a loaded body. It is classified as major principal stress and minor principal stress. On the plane of principal stress shear stress value is termed as zero.
When principal stress gets on the major principal plane, it is called major principal stress and when it is found on the minor principal plane, it is known as minor principal stress. These are denoted as σ1 and σ2, respectively.
Principal Stress Theory
Shear stress is a sloping applied force that causes deformation due to lateral load. In any stress block surface, there is applied shear stress over the plane, but to stabilize the body there, we need to apply complementary shear stress. This is known as complementary shear stress.
The principle of complementary shear stress is when the same intensity but opposite direction shear stress is applied over the surface of the body, it creates a couple and this couple stabilizes the body. This balancing couple mechanism is known as the principle of complementary shear stress.
What is Maximum and Minimum Principal Stress?
Principal stress is calculated on the principal plane as maximum stress is called major principal stress, and minimum stress on the principal plane is called minor principal stress.
Here;
- σx = Stress in x direction
- σY = Stress in the Y direction
- τn = Normal shear stress
- Ө = inclination angle of stress to the principal axis
- X and Y are the axes of the plane.
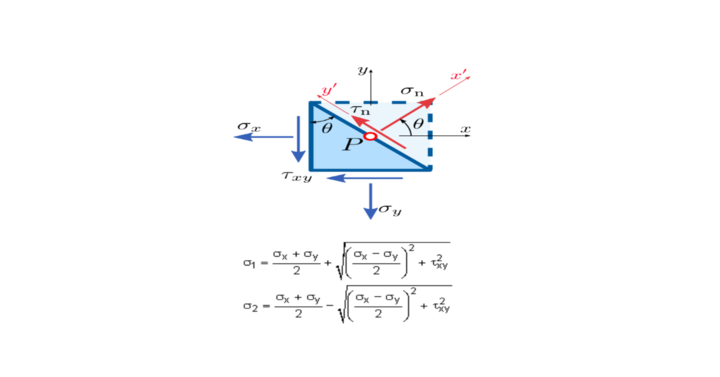
Where
- σ1 is the maximum principal stress, and
- σ2 is the minimum principal stress. it is also termed as σMaxand σMin.
Maximum shear stress (τmax) = (Maximum principal stress- Minor principal stress)/2 =R
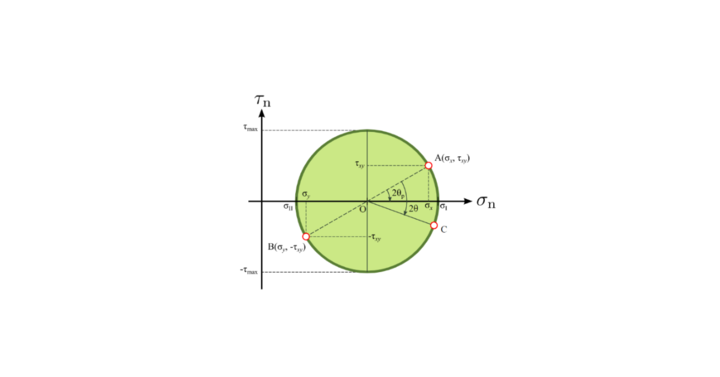
Here maximum shear stress is the magnitude of that point with an equal radius in a mohr circle, and principal stress is the end point of the circle’s diameter.
Here we take only two-dimensional theory in which we consider σ1 ( the maximum principal stress ) and σ2 (the minimum principal stress). But in the case of three-dimensional theory, we take σ1, σ2 and σ3. In this case, we decide on the major or minor principal stress by using principal stress theory or Rankine, lames or maximum principal stress theory.
Maximum Principal Stress Theory
When the applied load needed to be calculated under the design criteria, the total applied load should be less than the ultimate yield capacity of material divided by the factor of safety. This theory is also a part of principal stress theories and its also known as Rankine’s theory, lame’s theory and reciprocal theory.
According to the maximum principal stress theory-
σ1 + σ2 + σ3 ≤ yield strength/Factor of safety
Principal Stress and Principal Strain
Principal stress is related to the existing principal plane available stresses as when stress is line on maximum principal planes as positive and negative stress value higher in magnitudes called principal stress. Stress is a tensor because it follows the transformation equation.
In principal strain the maximum and minimum normal strains are obtained by differentiating x, and y coordinates and the orientation of the planes of the strains is determined there are two roots, p1 and p2, for 1 and 2 directions. Principal strains are the nominal strains with higher magnitude.


