Moment Area Method
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In the civil engineering design of structures, various parameters are used to design structures. These parameters consist of bending moment, slope, deflection, shear force, etc. Many methods are available for finding the slope and deflection of beams, like the double integration method, Macaulay’s method, the Conjugate beam method, etc. The moment area method is among those methods for finding these parameters of structural analysis. The moment area method is used especially for the non-prismatic beams. Non-prismatic beams are beams that have varying cross-sections along their span.
Moment Area Method PDF [GATE Notes]
The moment area method is based on the two theorems known as the moment area theorem. These theorems are based on the Moment of the area of the bending moment diagram about its center. With the help of these theorems, the slope and deflections of beams and other structures are determined. The moment area method is generally used in the case of non-prismatic beams, but it can also be used for prismatic beams.
Table of content
What is Moment Area Method?
The Moment area method for finding the slope and deflection of the beam is the most appropriate method for calculating the effect of branding over the beam. This method can be used for prismatic and non-prismatic beams, but the calculation of deflections by moment area method for non-prismatic beams gets easier hence it is preferred in this case.
In the moment area method, the area moment of the bending moment diagram about a particular point is utilized to calculate the slope and deflection. The moment area method can be used in the case of internal hinges or links because, in such cases, sudden changes in slope will occur. These limitations will be clear after understanding the moment area theorems.
Moment Area Method is Applied to Determine
The moment area method can be used for prismatic and non-prismatic beams. Due to its uses, it becomes more useful than other methods like the double integration method and Macaulay’s methods. The moment area method is applied to determine the slope and deflection of beams or frames. This method is proven easier than the other methods for complex problems.
The moment area method is also known as Mohr’s method. This method assumes that the slope of beams or frames varies continuously; it can’t b applied in case of a sudden change in slopes. This method is preferred for non-prismatic beams due to its advantages. This method becomes very difficult to find slope or deflection when the point of zero slopes in the beam or frame can not be easily found because this method gives the relative slope of a point to another.
Download Formulas for GATE Mechanical Engineering – Machine Design
Moment Area Method Theorems
As we know, the moment area method applies to prismatic and non-prismatic beams. It is suitable when the point of zero slopes and zero deflection is known.
Thus, it is unsuitable when internal hinges are present because the internal hinge slope suddenly changes. This method is based on the two theorems described below.
Theorems of moment area method:
Theorem 1: Change in slope from any point x to B is equal to the Area of the M/EI diagram between x and B.
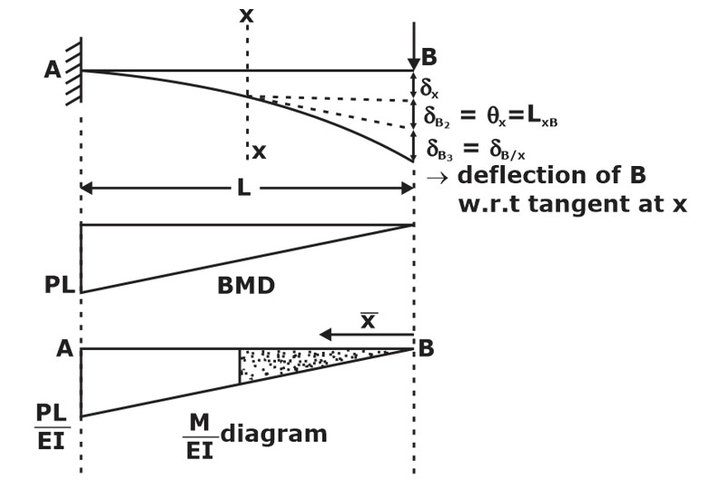
Mathematically,
θxB = θB – θx =Area of diagram between x and B
If the point of zero slopes is known (A), then the change in slope from A to B equals the Area of the M/EI diagram between A and B.
θAB = θB – θA = Area of M/EI diagram between A and B
But θA = 0, So
θB – 0 = -(1/2) L (PL/EI)
⇒ θB = – (PL2/2EI)
Theorem 2: The deflection of any point B, w.r.t tangent at any point x (δB/x) is equal to the moment of Area of M/EI diagram between x and B about B.
δB/x = moment of Area of M/EI diagram between x and B about B
δB/x = Ax¯
By the above diagram,
Total deflection of B = δB1+δB2+δB3
BB1 = ΔB = δx + θx LxB + Ax¯
Moment Area Method for Slope and Deflection
In structural analysis, many methods are available to calculate the slope and deflection of beams or any other structural members. The use of all methods depends on the suitability of the methods and other conditions like loading, type of beams, etc. Different methods for finding the slope and deflection are mentioned below:
- Moment Area Method
- Double Integration Method
- Macaulay’s Method
- Strain Energy Method
- Conjugate Beam Method
The moment area method is based on the moment area theorems. This method is mainly used for non-prismatic beams but can also be used for prismatic beams. Here is a short comparison of other methods:
The Conjugate beam method is used in complex loading conditions; It converts the real beam into a conjugate beam by changing its supports such that the deflection and slope of the real beam are equal to the bending moment and shear force of the conjugate beam, respectively.
The double integration method is the general procedure of solving slope and deflection problems, and Macaulay’s method simplifies the double integration method.
And strain energy method for calculating the slope and deflections of the beams is based on the concept of strain energy; it uses Castigliano’s theorem for calculating these parameters.
Moment Area Method for Cantilever Beams
The moment area method is a method for finding the slope and deflection of a beam. This is more suitable in non-prismatic beams because, in the case of such beams, the flexural rigidity of the beam changes suddenly, and other methods become complicated. Still, slope and deflection by this method can be easily solved as this method requires a M/EI diagram. Because of this advantage of this method, it can be used for any type of beam or loading.
So, in the case of a cantilever beam, the slope and deflection equation depend on the type of loading over the beam. Only the way of calculating these parameters will depend on the type of method used. Finding the slope and deflection by moment area method for fixed beams gives an extra condition that the slope and deflection at the fixed support will be zero. This condition has some advantages in this method, like the slope of any in-between point of the beam can be calculated relative to the fixed support, and it is the same as the required slope; no extra calculation is required.
Moment Area Method Problem and Solutions
As we know, the moment area method is the method for finding the slope and deflections of a beam; it is mainly used for prismatic beams but can be us for non-prismatic beams. This method’s concept becomes clearer by solving a question based on this. Here such an example is given for the non-prismatic beams, which makes a better understanding of the related concepts.
Example: Using the area moment theorem, find the slope and deflection at the free end for the beam shown below:
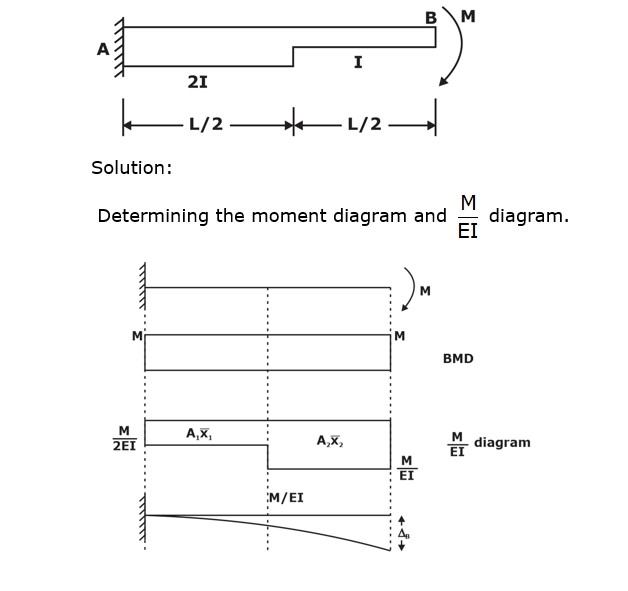
Change in slope from A to B,
θAB = θB – θA = θB

Download Formulas for GATE Mechanical Engineering – Fluid Mechanics and Machinery


