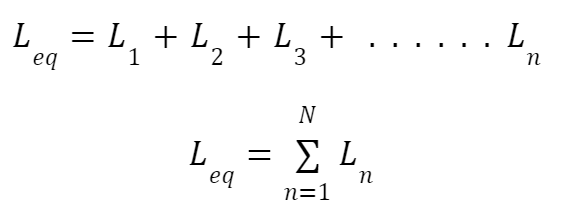Inductors in Series

Inductors in Series

The interconnection of inductors in series is a part of any complex network that can be reduced to a simple network by an equivalent inductor in series whose inductance is the sum of the individual inductors in series with no mutual inductance.

When inductors are connected in series, there is a certain voltage drop across each inductor for a given rate of change of current passing through it. For the rate of change of current, the greater the voltage drop means, the greater the inductance of the inductor.

Download Formulas for GATE Electronics & Communication Engineering – Digital Circuits

Equivalent Inductance of Inductors in Series

Consider a series connection of N inductors having equivalent circuits, as shown below. The same current flows through all the inductors as they are in series.

If a current I is flowing through an inductor having inductance L, the voltage V across the inductor is equal to, 

Inductors in series are similar to that resistors in series. The equivalent inductance is the individual sum of all inductances when inductors are connected in series.

Download Formulas for GATE Electronics & Communication Engineering – Electronic Devices

Mutually Coupled Inductors in Series

The magnetic field of one inductor links with the other inductor when connecting the inductors in series. This phenomenon is known as magnetic coupling. This leads to either decreasing or increasing the overall equivalent inductance. Based on the aiding or opposing the overall equivalent inductance, they are classified as

• Differentially coupled or series of opposing
• Cumulatively coupled or series aiding

If the magnetic flux produced by the current through the inductors is in the opposite direction, it is differentially coupled because it will oppose the overall equivalent inductance. So, the overall equivalent inductance will decrease.

Suppose the magnetic flux is in the same direction. In that case, it is cumulatively coupled because it will aid the overall equivalent inductance, increasing the circuit’s net inductance.

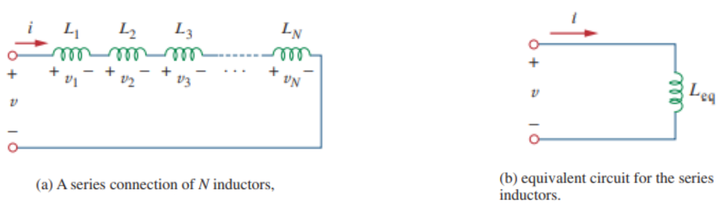
Differentially Coupled Inductors in Series

In this type of connection of connecting inductors in series, the direction of current entering or leaving at the terminal of an inductor is in the opposite direction, as shown below:

 

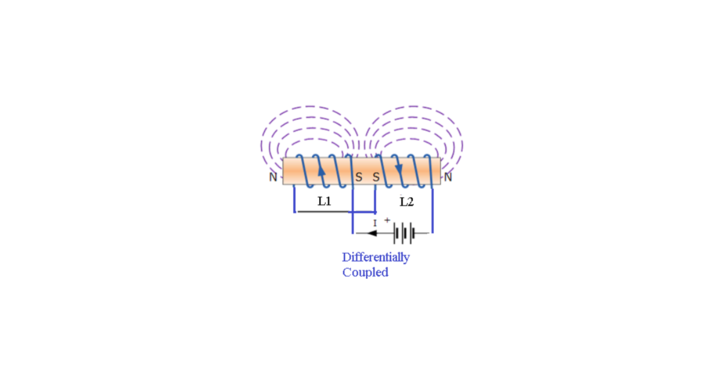
Let M be the mutual inductance due to magnetic coupling between the inductance L₁ and L₂. The electric circuit representation can be drawn as:

Cumulatively Coupled Inductors in Series

On connecting Cumulatively Coupled Inductors in series, the direction of current entering or leaving at the terminal of an inductor is in the same direction as shown below:

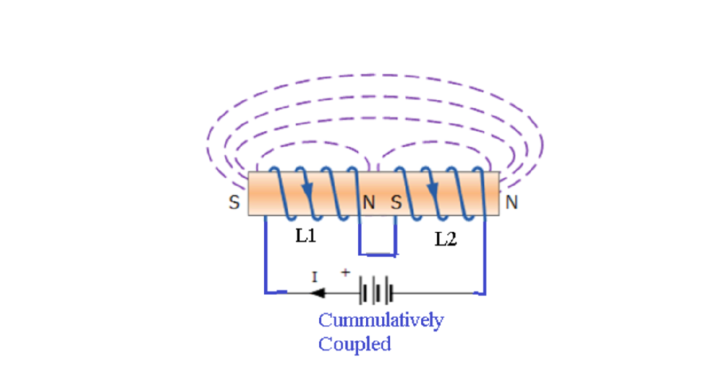
Let M be the mutual inductance due to magnetic coupling between the inductance L₁ and L₂.

Inductors in Series Formula

When N number of inductors are connected in series (assuming no magnetic coupling), then the overall equivalent inductance is the sum of the individual inductance present in the circuit. Mathematically, Inductors in the series formula can be written as:

Important GATE Topics
Torsion Equation	Boolean Algebra Laws
Storage Class In C	Number System Questions
RSA Full Form	Difference Between Join And Union In Sql
Difference Between Clustered And Non-Clustered Index	Difference Between Commit And Rollback In Sql
Difference Between Multithreading And Multitasking	Types Of Stress