- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Incidence Matrix
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The Incidence Matrix describes which branches are incident at which nodes and what are the orientations relative to the respective nodes. This incidence matrix is also termed a complete incidence matrix. Graph theory, often known as network topology, is concerned with network features that do not change when the geometry of the network changes. The equations created by the graph theory concept (KCL and KVL) are independent equations.
The graph theory concepts make it easier to solve networks with a high number of nodes and branches. The article elaborates on the incidence matrix, properties of the incidence matrix, reduced incidence matrix, and some examples.
Table of content
What is the Incidence Matrix?
In graph theory, while drawing a graph, all the passive elements of a network are represented by lines. The independent voltage and current source are replaced by their internal impedance (independent voltage source-short circuit and independent current source-open circuit).
Incidence Matrix Definition
The incidence matrix represents a network symbolically. It also makes testing and identifying the independent variables easier. An incidence matrix is a matrix that uniquely represents a graph.
What are the Dimensions of an Incidence Matrix?
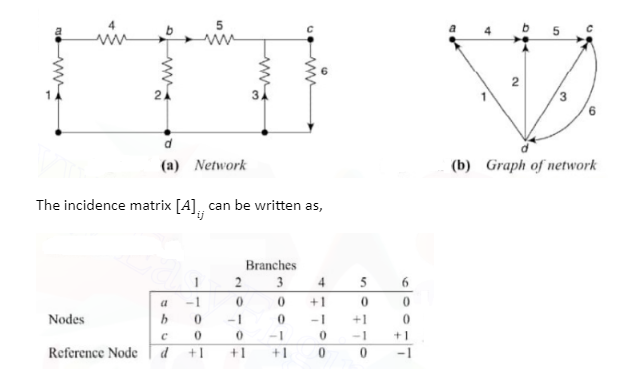
For a graph of n number of nodes and b number of branches, the complete incidence matrix [A]ij will be a rectangular matrix of order n×b.
[A]ij =1; if branch j is associated with node i and oriented away from node i
[A]ij =-1; if branch j is associated with node i and oriented towards from node i
[A]ij = 0; if branch j is not associated with node i
How to Find the Incidence Matrix of a Graph?
Consider a network having 6 branches and 4 nodes as shown below. Node d is taken as a reference node. The equivalent graph of the network is also drawn as shown below. The order of the incidence matrix will be 4×6.
Properties of Incidence Matrix of a Graph
A complete incidence matrix [A]ij a graph has some properties by which one can identify whether the given matrix is a complete incidence matrix or not. These properties are:
- The sum of values of [A]ij of any column is equal to zero.
- For a closed loop system, the determinant of [A]ij is always zero.
- The rank of the complete incidence matrix [A]ij is n-1 where n=number of nodes in the graph.
Reduced Incidence Matrix of a Graph
The matrix which is obtained from the complete incidence matrix by eliminating one of the rows is known as the reduced incidence matrix. Generally, the reference node is eliminated from the complete incidence matrix to form a reduced incidence matrix.
The reduced incidence matrix is represented as [Ar]ij. Reduced incidence matrix is used to find the number of trees for connected graphs. The number of trees is calculated by taking the determinant of the product of the reduced incidence matrix with its transpose as shown below:

Incidence Matrix and KCL
Consider a random graph as shown below. The branch currents are i1, i2, i3, i4, i5, and i6 for respective branches. For a graph having n nodes, then, from the incidence matrix we can get n-1 independent KCL equations.

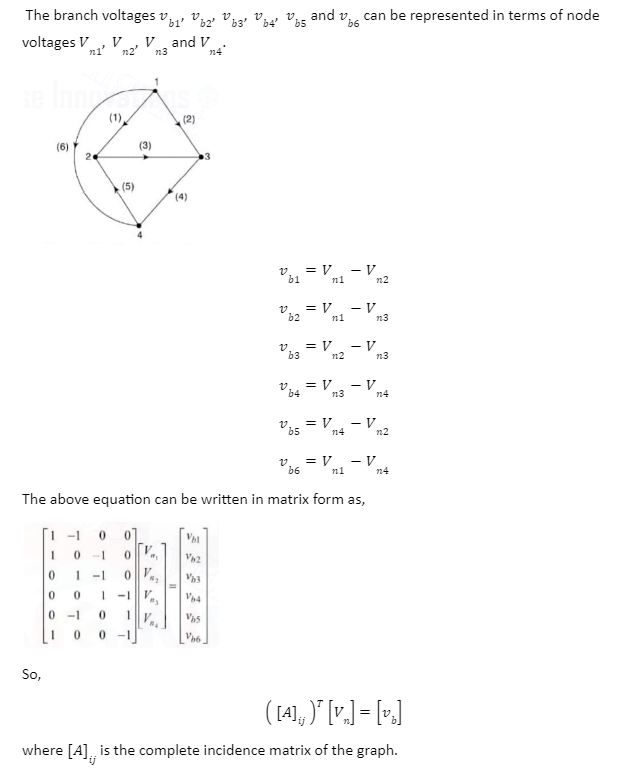
Incidence Matrix and KVL
Consider the same graph used in the incidence matrix and KCL as shown below.
Incidence Matrix Example
Example 1: Find the possible number of trees for the graph shown below.



