- Home/
- GATE CE/
- ESE (IES Exam) CE/
- Article
Stress Distribution in Soil
By BYJU'S Exam Prep
Updated on: September 25th, 2023

The stress distribution in soil depends on the depth of the point of consideration, and it will also depend on the radial distance of the point of load. The article contains fundamental notes on the “Vertical Stress Distribution in Soil” topic of the “Geotechnical Engineering” subject.
Stress Distribution in Soil PDF
This topic covers the increment of stress in the soil due to applied load over the soil. And the discussion of vertical stress distribution in soil has been carried out with the help of Boussinesq’s and Westegaurd’s theory.
Table of content
What is the Vertical Stress Distribution in Soil?
At a point within a soil mass, stresses will be developed due to the soil lying above the point and by any structural or other loading imposed onto that soil mass. Vertical stress distribution in the soil is one of the important topics of the GATE Civil Engineering syllabus. Stress in the soil may be caused by the following:
- Self-weight of soil
- Applied load on the soil
Vertical stress distribution in the soil means the stress distribution beneath the soil layers when it is subjected to loading over the topsoil. Vertical stress depends on the depth of the point below the layer of the soil and the radial distance from the point of application of loading. The load distribution over the soil can occur in different forms like strip loading, circular loading, etc. Here a few distributions are shown below.
Finitely Loaded Area
If the surface loading area is finite (point, circular, strip, rectangular, square), the vertical stress increment in the subsoil decreases with an increase in the depth and the distance from the surface loading area.
Methods have been developed to estimate the vertical stress increment in sub-soil considering the shape of the surface loading area.
Boussinesq’s Theory of Vertical Stress Distribution in Soil
Different methods are available to determine the vertical stress distribution in the soil. Boussinesq’s theory applies only to the point load, and it consists of the following assumptions:
Point Load
A point load or a Concentrated load is, strictly speaking, hypothetical in nature; consideration of it serves a useful purpose in arriving at the solutions for more complex loadings in practice.
Assumptions of Boussinesq’s Theory
Boussinesq’s theory is used to determine the vertical stress at a point below the top layer of soil due to the action of point load over it. It consists of the following assumptions:
(i) The soil medium is an elastic, homogeneous, isotropic and semi-infinite medium, which is infinitely in all directions from a level surface.
(ii) The medium obeys Hookes law.
(iii) The self-weight of the soil is ignored.
(iv) The soil is initially unstressed
(v) The soil’s volume change upon application of the loads onto it is neglected.
(vi) The top surface of the medium is free of shear stress and is subjected to only the point load at a specified location.
(vii) Continuity of stress is considered to exist in the medium.
(viii) The stresses are distributed symmetrically with respect to the z-axis.
The equations for the stress distribution can be expressed as follows:
This intensity of vertical stress directly below the point load, on its axis of loading (r=0), is given by:
σz = 0.4775 Q/Z2
Vertical Stress Distribution on a Horizontal Plane
The vertical stress on a horizontal plane at depth z is given by
σz = KB Q/Z2
Westergaard’s Theory of Vertical Stress Distribution in Soil
Westergaurd’s theory also determines the vertical stress below the topsoil. These theories have been proposed based on certain assumptions for which it is valid. According to this theory, vertical stress can be calculated per the following equations.
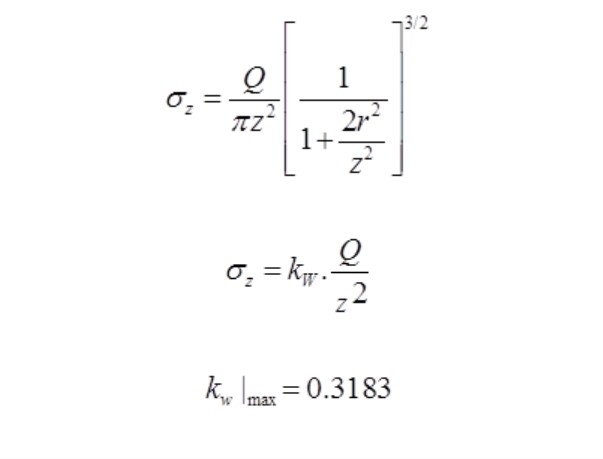
Westergaard’s Results
(i) Vertical stress due to Live Loads
σz = (2q’/πz) [1/{1 + (X2/Z2)}]2
where, σz = Vertical stress of any point having coordinate (x, z)
Load intensity = q’ per m
at X = 0; σz = 2q’/πz
(ii) Vertical Stress due to Strip Loading

where σz = Vertical stress at point ‘p’

(iii)σz = (q/π) [β + sinβ] for strip loading having angle βfrom its edge.
(iv) Vertical stress below uniform load acting on a circular area.
σz = q(1-cos3 θ)
where cos θ = z / (r2 + z2)
Newmark’s Chart Method
Newmark’s chart method is a graphical method for determining the vertical stress due to any type of loading over the soil. It is generally preferred in case of uniform loading over irregular areas. Here few points about Newmark’s chart method are given below.
- Newmark (1942) constructed an influence chart based on the Boussinesq solution to determine the vertical stress increase at any point below an area of any shape carrying uniform pressure.
- This method applies to semi-infinite, homogeneous, isotropic and elastic soil mass. It does not apply to layered structures.
- The greatest advantage of this method is that it can be applied to a uniformly distributed area of an irregular shape.
- The chart consists of influence areas with an influence value of 0.005 per unit pressure.
- Position the loaded area on the chart such that the point at which the vertical stress is required is at the centre of the chart.
- Newmark’s chart is made of concentric circles and radial lines. Normally there are 10 concentric circles and 20 radial lines.
Influence of area (1) = Influence of area (2) = Influence of area (3)
Influence of each area = (1 / Total number of sectoral area) = 0.005
σz = 0.005qNA
Where NA = The total number of sectorial areas of Newmark’s chart.

If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE:
Online Classroom Program for ESE/GATE CE
For more information on the topic, refer to the following video on Byju Exam Prep’s official youtube channel.
 Daily GATE & ESE Live Sessions, Free Live Classes, Study Notes, Quizzes & Free PDF’s & more, Join our Telegram Group Join Now
Daily GATE & ESE Live Sessions, Free Live Classes, Study Notes, Quizzes & Free PDF’s & more, Join our Telegram Group Join Now You can avail of BYJU’S Exam Prep Test Series, specially designed for all Civil Engineering Exams:


