- Home/
- GATE CE/
- ESE (IES Exam) CE/
- Article
Ground Water Hydrology
By BYJU'S Exam Prep
Updated on: September 25th, 2023

Through Champion Study Plan for GATE Civil Engineering (CE) 2022, we are providing Ground Water Hydrology study notes and other important materials on every topic of each subject.
These topic-wise study notes are useful for the preparation of various upcoming exams like GATE Civil/ IES/ BARC/ ISRO/ SSC-JE/ State Engineering Services examinations and other important upcoming competitive exams.
The article contains fundamental notes on the “Ground Water Hydrology” topic of the “Engineering Hydrology” subject.
Table of content
Ground Water Hydrology
Aquifer
An aquifer is an saturated geological formation, underground layer of water-bearing permeable and porous or unconsolidated materials (gravel, sand, or silt) from which groundwater can be extracted using a water well.
Some Fundamental definitions:
1) Aquiclude
- These are the geological formations which, are highly porous but non-permeable. Hence water cannot be extracted from these types of geological formations.
e.g. Clay
2) Aquitard
- These are the geological formations, which are porous but possess very less permeability. Hence water does not readily flow out of these formations, but instead water seeps out.
e.g. Sandy Clay
3) Aquifuge
- These are geological formations, which are neither porous nor permeable.
e.g. Granite
Type of aquifer
- Un-Confined aquifer
- Perched aquifer
- Confined aquifer

Figure Groundwater profile or aquifer system
1) Un-confined aquifer
- Boundary of Un-confined aquifer extended from water table (water surface which is under atmospheric pressure) to impermeable bed strata.
- Not subjected to any confining pressure and Water in Un-confined aquifer is under atmospheric pressure.
- Un-confined aquifer are recharged by directly rainfall over the surface and water body.
- This aquifer is also called non-artesian aquifer.

Figure Various type of Un-confined aquifer
2) Perched aquifer
- Perched aquifer is small water body which is situated in unsaturated zone of soil above the main ground water table or main unconfined aquifer, separated by impervious strata.
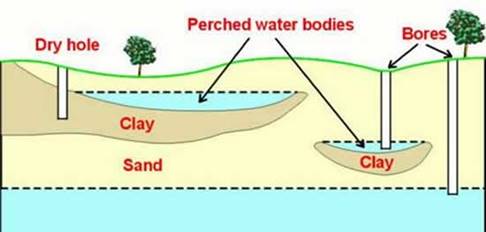
Figure Perched aquifer
3) Confined aquifer
- Confined aquifer bounded between two impermeable or very less permeable soil strata or rocks.
- In confined aquifer, water is under pressure or artesian pressure (pressure above the atmospheric pressure) because in that case water is sandwiches between to impermeable layer or rock.
- This is also called artesian aquifer.

Figure Confined aquifer
Some important terminology used in well hydraulics
1) Cone of depression
- Cone of depression represent the water table during the drawdown of water with the help of well through homogeneous and isotropic aquifer.
- In un-confined aquifer cone of depression represent the drawdown water table but in confined aquifer it represent the pressure drop (change in piezometric head) around the well.
- Drop in water table from previous static water table is termed as drawdown depth or simply drawdown.

Figure 3-d view of cone of depression

Figure Cone of depression in Un-confined aquifer

Figure Cone of depression in confined aquifer
2) Radius of influence
- It is the maximum distance up to the effect of drawdown is detected.
- In other word, radius of influence represent the radial extent of cone of depression. And areal extent represent by area of influence.

Note:
- When we start drawdown from well, initially the drawdown surface not constant and changes with time (due to unsteady flow). After sufficient time equilibrium state is reached and flow become steady.
- After attaining equilibrium state there is no change in drawdown surface, drawdown surface become constant with respect to time.
- And after stopping pumping, accumulation of water in influence zone started and this phenomenon termed as recuperation or recovery of well.
Different way of extracting water
1) Infiltration Galleries
- These are horizontal tunnels constructed at shallow depth of the 3-5 m along the bank of river in water bearing strata.


Derivations:
Discharge through element
qx = ax*vx
= (h*L)*k*ix (by Darcy’s law V= k*ix)
= h*L*K* dh/dx
Total Discharge
Q= ∫qx
= ∫h*L*k*dh/dx

Q*R = k*L* [H2– h02]
Q = kL(H-h0)(H+h0)/(2R)
2) Infiltration Well
- These are discontinuous structure constructed along bank of river in which water is collected through seepage from bottom.
- All such wells are connected through a common well known as Jack well from which water is pumped to treatment plant.
3) Artesian Spring
- Artesian spring have potential sources of raw water, while non-artesian spring are not potential sources. Because in summer water table may get depleted.

4) Well
These are generally of two types
- Open Wells
- Shallow well
- Tube well
- Tube Wells
- Screen type
- Cavity type
1) Open Wells
- In shallow well water is drawn from top most water bearing strata, which is liable to be contaminated.
- Large quantity of water cannot be extracted from shallow well as with increase in discharge, velocity of flow through well increase and if this velocity exceeds critical velocity (velocity at which medium particles starts moving with flowing water settling velocity) leads to destabilisation of well lining and finally resulting in piping. This process is known as “Piping”. Sinking of well is consequences of piping.
- This problems does not occur in deep well, as with increase in discharge, when velocity through well increase resulting in the movement of medium particles from bottom of the well leading to increase area of flow from bottom. This process is known as cavity formation.
- Due to this increase area of flow velocity through the well again decrease which finally results in no movement of medium particles along with the water.
- In case of deep wells, destabilisation of well lining does not take place even after piping occurs as well lining is being supported by impervious layers.

Open Well Yield
Recuperating test
- Also known as equilibrium pumping test.
- This test is performed to get approximate yield from open well.
- In this test pumping is done up to working head (one third of critical depression head) for subsoil. Say S1 Critical depression head- depression head at which loosening (quick sand phenomenon) of sand surrounding the well start.
- After that pumping is stopped and allowed to rise the water level in well or allow to recover the water head in well. And recuperation depth and corresponding time is noted for calculation of yield from well. Say recuperation depth = S, and corresponding time = T

Derivation Part-1
Let water level rises in well from s1 to s2 in T time
According to Darcy’s law
“For laminar flow through saturated soil mass, the discharge per unit time is proportional to the hydraulic gradient”.
Q = K.i.A ———- (1)
i = Hydraulic gradient = s/L ———– (2)
(Head s is lost in a length L of seepage path)
If ds is the water level rises in well in dt time than
Q dt = –A ds
Negative sign indicate the decrease in depression head with time during the recuperation of well.
From equation 1, 2 and 3
![]()
Integrating them

Where ![]() a constant C and it is the specific yield of well. Dimension C is T-1.
a constant C and it is the specific yield of well. Dimension C is T-1.
So equation 4 become

Derivation Part-2
The yield of the well is
Q = CAH
Assumption: entire flow in well is from the bottom of well (impervious steining of masonry)
Where Q = safe yield of the well
A = area of cross section of the well
H = safe working depression head
C = specific yield of the well
Specific yield:-
Specific yield soil is defined as discharge per unit area under a unit depression head (drawdown).
Steady flow into a well
Case-1: Well in Confined Aquifer. (Theim’s theory)
Assumptions:
- Medium is assume to be homogeneous and isotropic
- Flow of water in the vicinity of well is radial horizontal and laminar.
- The loss of head is directly proportional to tangent of hydraulic gradient (dh/dx) instead of (ds/dx) .

In this figure
rw = radius of well, b = thickness of confined aquifer
sw = Drawdown
hw = Piezometric head at pumping well
H = original piezometric head or piezometric head before staring pumping
hr, sr = piezometric head and draw down of water table at distance r from centre of well
h1, s1 = piezometric head and draw down of water table at distance r1 from centre of well
h2, s2 = piezometric head and draw down of water table at distance r1 from centre of well
According to Darcy’s low
Velocity of flow at radial distance r
![]()
Here ![]() is hydraulic gradient (dh is head loss over dr radial distance)
is hydraulic gradient (dh is head loss over dr radial distance)
Discharge from well Q = Vr x A {A = cylindrical surface area through which water enter into well}
A= 2πrb

By integrating it

if H is the original piezometric head, hw = piezometric head at well,
R = Radius of influence, = 3000Sw√K, K= Permeability of Soil,
rw = radius of well

Above equation represent the discharge from pumping well for steady flow condition.
s1= H-h1; s2= H-h2 ——– (6) (see above figure)
And T= Kb ——- (7)
Note: T is Transmissibility and it defined as flow capacity or discharge of aquifer per unit width under unit hydraulic gradient. T has the dimension of [L2/ T ] .
From equation 5, 6 and 7

Note: above equation is valid only for steady state flow condition and for well having complete penetration in aquifer
Case-1: well in unconfined aquifer.

In this figure
rw = radius of well
sw = Drawdown
hw = Piezometric head at pumping well
H = original piezometric head or piezometric head before staring pumping
hr, sr = piezometric head and draw down of water table at distance r from centre of well
h1, s1 = piezometric head and draw down of water table at distance r1 from centre of well
h2, s2 = piezometric head and draw down of water table at distance r1 from centre of well
According to Darcy’s low
Velocity of flow at radial distance r
![]()
Here ![]() is hydraulic gradient (dh is head loss over dr radial distance)
is hydraulic gradient (dh is head loss over dr radial distance)
Discharge from well Q = Vr x A {A = cylindrical surface area through which water enter into well}
A = 2πrh

By integrating it

Above equation represent the discharge from pumping well for steady flow condition.
At r = R radius of influence
r2 = R, r1 = rw than h1 = hw, h2 = H

If sw = (H- hw) is small compare to H than

From equation 10, 11

Transmissibility T= Kb ——- (13)

s1 = H-h1; s2 = H-h2
Put the value of s1 and s2 in equation (9)

Note: above all equation of Q is valid only for steady state flow condition and for well having complete penetration in aquifer
Well losses and specific capacity –
Head loss (drawdown) due to flow through soil pours, screen and in the well.
1) Drawdown (sw) in a pumping well has three component like
1) Formation loss- head loss due to flow through porous media. (swL)
2) Head Loss due to turbulent flow near screen. (swt)
3) Head loss due to flow through screen and casing. (swc)
- Formation loss swL ∝ discharge Q
- swt ∝ Q2
- swc ∝ Q2
So


Figure well loss in confined aquifer
Specific capacity
- Discharge per unit drawdown known as specific capacity of well.
- Specific capacity indicates the performance of well.
So specific capacity (if well losses are ignored)

Example: (from engineering hydrology by k. subramanya)
Given
1) Radius of pumping well rw = 15 cm
2) Aquifer depth = 40 m
3) Steady state discharge = 500 lpm = 
4) Drawdown at two observation well
1. 25 m away from pumping well
r1 = 25 m
s1 = 3.5 m it means h1 = (40.0 – 3.5) = 36.5 m
2. 75 m away from pumping well
r2 = 75 m
s2 = 2 m it means h1 = (40.0 – 2) = 38 m
5) It is given that, the well is fully penetrated in aquifer.
Find
- Transmissivity (T)
- Drawdown at pumping well (sw)
Solution:
1) Discharge from well

Put the known value in formula

K = 7.823 x 10-5 m/s
We know that Transmissivity T = K x H
T = {7.823 x 10-5 m/s} {40 m}
T = 3.13 x 10-3 m2/s
2) 
Put respective numerical values in above formula

By solving that expression
hw = 28.49 m and from that hw, sw = 40-28.49 = 11.51 m
*****
If you are preparing for ESE/ GATE or other PSU Exams (Civil Engineering), then avail Online Classroom Program for ESE and GATE CE:
Online Classroom Program for ESE/GATE CE
You can avail of BYJU’S Exam Prep Test Series specially designed for all Civil Engineering Exams:
BYJU’S Exam Prep Test Series ESE/GATE CE
Thanks
All the Best


