Muller Breslau Principle: Application, Advantages, Examples
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In civil engineering structural analysis, it is very important to know the position of critical sections. These sections may be critical regarding shear force, bending moment or other stress functions. The concept of an Influence Line Diagram (ILD) is used to know the critical sections for the moving load condition. These influence line diagrams can be determined with the help of the Muller-Breslau principle. According to Muller Breslau’s principle, ILD for any structural member’s stress function can be determined easily.
Muller Breslau’s Principle PDF
Muller Breslau principle in structural analysis is used for the determination of Influence line diagrams for a structural member. The Muller-Breslau principle can be used to determine the ILD for determinate and indeterminate structures. In this article, we discuss Muller Breslau’s principle and the determination of ILD with this principle.
Table of content
What is Muller Breslau Principle?
Muller Breslau principle is an important principle of structural analysis used for determining the influence line diagram for a stress function of a member. According to the Muller Breslau principle, “If an internal stress component or reaction component is considered to act through and tends to deflect a structure, then the deflected shape of the structure will be the influence line for the stress or reaction component to some scale.” This principle assumes the scaled form of displacement for calculating influence line diagrams.
An influence line diagram for a stress function can be calculated by an analytical approach as well. But with the help of Muller Breslau principle, it can be found just simply deforming the member by the unit deformation in the same direction as the effect of stress functions. Muller Breslau principle can be used to form the MSQ-based questions in the GATE CE question paper. This principle can be applied to beams, trusses, frames, etc., to determine the ordinate of the influence line diagram.
Application of Muller Breslau Principle
The Muller Breslau principle is applicable for determining the influence line diagram for the determinate or indeterminate type of structures. The Muller Breslau principle is based on the concept of the deflection curve. It assumes that the influence lines are the elastic deflection curve of a member. Muller Breslau principle is important for the GATE CE exam. This principle is based on the theorem of Maxwell’s reciprocal theorem and Betti’s law.
Muller Breslau principle is applied to beams to evaluate the ordinate of influence line diagrams used to define the critical sections. It can be used for making the influence line diagrams for any stress functions like shear force, bending moment, reactions at supports, etc.
Advantages of Muller Breslau Principle
Determination of Influence Line diagrams can be possible with the help of an analytical approach in which one unit load is moved from one end to another end of the member, and values for any stress functions are calculated across the span of the members in terms of the distance from one end of the member to the other. But with the help of the Muller-Breslau principle, it is possible to calculate easily. Muller Breslau principle It becomes easy only due to its advantages listed below:
- Muller Breslau’s principle uses the elastic deflection approach to calculate ILDs.
- It can be used for both determinate and indeterminate structures.
- This is the simplest approach to drawing the influence line diagrams for a particular stress function.
Download Formulas for GATE Civil Engineering – Environmental Engineering
Determination of ILD by Muller Breslau Principle
Before drawing the ILD by Muller Breslau principle, Let’s first know about the influence line diagrams. These lines are important for the GATE exam and show the variation of stress functions for a point due to the moving unit load across its span. As we discussed, the Muller Breslau principle provides a simple procedure for finding the Influence line diagrams. Here is the step-by-step guide for finding the influence line diagrams with this principle.
First, introduce the unit load in the direction of the stress function and gives the same effect to the member as the stress function causes that. And draw the deflection curve for this condition of the load. To determine the influence line diagram for the shear force and support reactions, a unit point load will be applied on the member while the unit rotation is applied to determine ILD for the bending moment.
The influence line diagram will be the linear curve for the determinate structures, and it will be curvilinear in shape for the indeterminate structures.
Download Formulas for GATE Civil Engineering – Fluid Mechanics
Examples of Muller Breslau Principle
Muller Breslau’s principle is useful for determining a structural member’s influence line diagrams. Determination of ILD with the help of Muller Breslau principle will be clearer by solving an example from the questions based on the GATE CE syllabus. Here such an example is given, which makes the concept better.
Examples of Use of Muller Breslau principle:
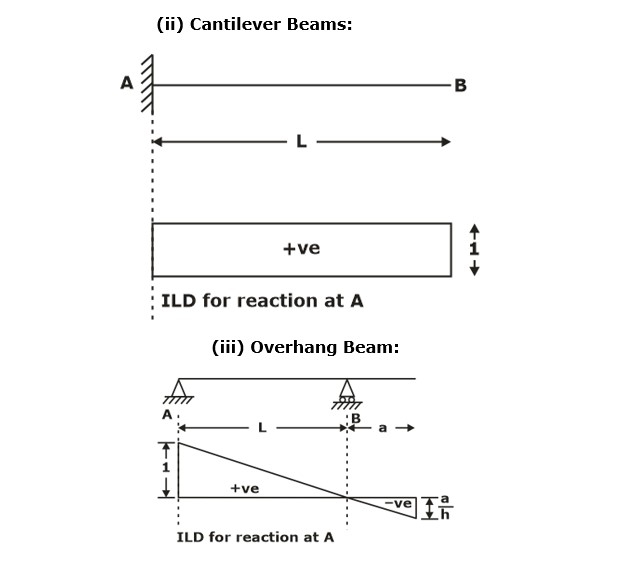
ILD for reaction at any support
To draw ILD for any reaction at support, remove the support and give unit displacement in the direction of the reaction. The deflected shape will be the ILD of that support.