- Home/
- GATE ELECTRONICS/
- GATE EC/
- Article
Electrostatics Notes & Topics for GATE EC/EE 2022
By BYJU'S Exam Prep
Updated on: September 25th, 2023

In this article, We will be sharing the notes on Electrostatics which will cover the major topics like Columb’s law, Electric field intensity, flux and Gauss’s Law, Electric Field and Potential.
Electrostatics: An electrostatics is a science related to the electric charge which is statics i.e., are at rest. Charge in terms of various charge distributions
![]()
where, ρL, ρS and ρV are line charge, surface charge and volume charge density respectively.
Charge Distribution: In electrostatics, we deal with point charges and different types of charge distributions like volume charge distribution, line charge distribution and surface charge distribution.
Volume Charge Distribution: It is defined as charge per unit volume.
![]()
where ΔQ is a small amount of charge in small volume ΔQ.
The total charge within a defined volume is obtained by taking the volume integral throughout the volume.
![]()
where, ρV = Volume charge density, and dV = Differential volume
Line Charge Distribution: In line charge distribution, while the charge is linearly distributed along the length of the line and it is defined by linear charge density. It is the charge per unit length.
![]()
![]()
where, ρL = Linear charge density, and dL = Differential length
Surface (Sheet) Charge Distribution: In surface charge distribution, the charge is uniformly distributed over the surface of a sheet and it is defined by surface charge density.
It is charge per unit surface area.
![]()
![]()
Here, ρS = Surface charge density, and dS = Differential area
Coulomb’s Law of Force:
Experiment has shown that a force exists between any two bodies that have a net electric charge, that is an excess of positive over negative charge or vice versa. When these bodies are called electrostatic. Such forces were studied by coulomb who experimentally determined a law about them.
If two charges of magnitude Q1 and Q2 respectively are situated on bodies whose dimensions are small compared to the distance, R, between them:
- Is proportional to Q1 Q2
- Is inversely proportional to R2
- Acts along the line joining the bodies, and
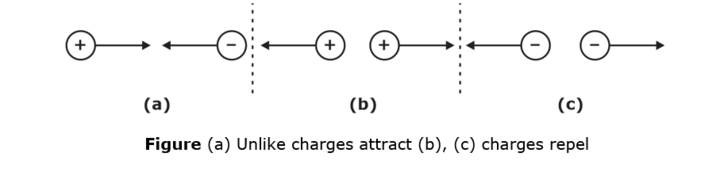
- Is attractive or repulsive according to whether Q1 and Q2 are of unlike or like signs respectively. Thus, the force experienced by Q2 due to the field of Q1 can be written as
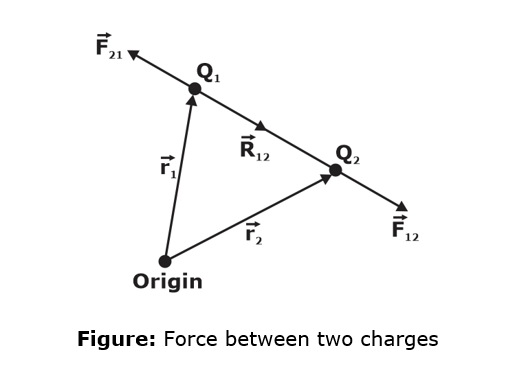

Note: The force is repulsive if Q1 and Q2 are of the same sign and attractive if they are of the opposite sign.
Electric Field Intensity: Force per unit charge is called electric field intensity (E).
![]()
![]()
where ρL is line charge density in C/m and r is radial distance.
![]()
where ρS surface charge density in C/m2 and an normal to the plane containing the sheet.
Electric Field due to Infinite Line Charge: Consider an infinitely long straight line carrying uniformly line charge having density ρL C/m. The electric field intensity at point P
![]()

Electric Field due to Uniformly Charged Ring: Consider a charged circular ring of radius r placed in XY plane with centre at the origin. Carrying a charge uniformly along its circumference. The charge density is ρL C/m.
Electric Field due to Infinite Sheet of Charge: Consider an infinite sheet of charge having uniform surface charge density ρS C/m2, placed in XY plane. We want to find E at point P present at Z-axis.



